Tìm số đo các góc \(A_1;A_2;A_3;A_4\), biết \(3A_1=7A_4\)
Hình minh họa...
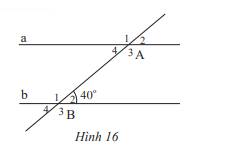
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
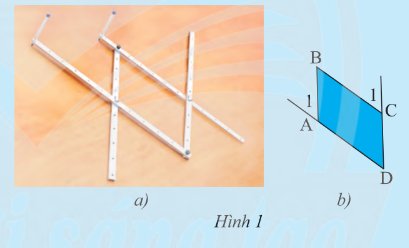
Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)
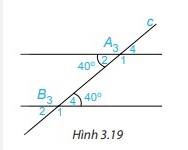
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
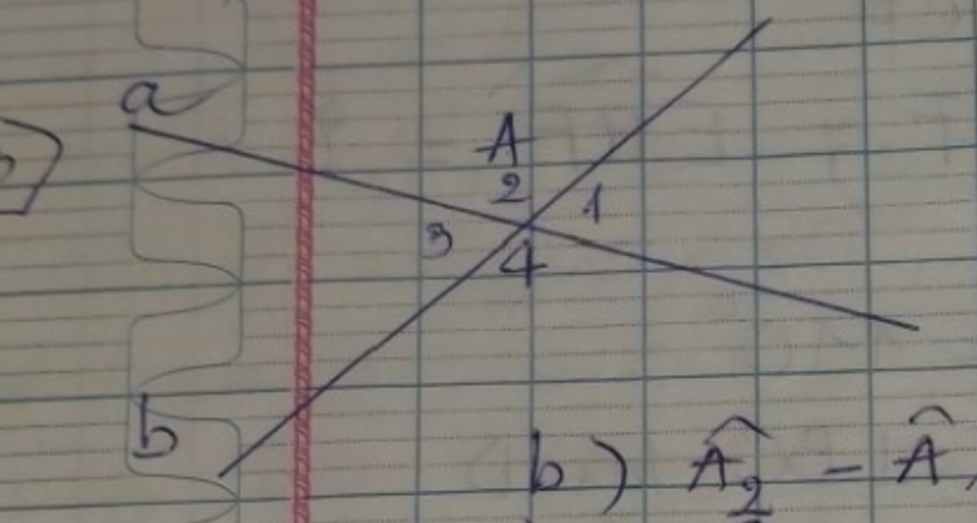
Xét các cặp góc đối đỉnh \(\widehat{_{A_1}}\)và \(\widehat{_{A_3}}\);\(\widehat{_{A_2}}\)và \(\widehat{A_4}\)được tạo thành khi hai đường thẳng a,b cắt nhau tại A .Tính số đo các góc \(_{A_1;A_2;A_3;A_4}\)trong mỗi trường hợp sau:
a) Góc A1+A3=\(120^O\)
b)\(3.\widehat{A_1}=7.\widehat{A_4}\)
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
a) Vẽ lại hình 15
b) Ghi tiếp số đo ứng với các góc còn lại
c) Gặp góc \(A_1,B_2\) và cặp góc \(A_4,B_3\) được gọi là hai cặp góc trong cùng phía
Tính :
\(\widehat{A_1}+\widehat{B}_2;\widehat{A_4}+\widehat{B}_3;\)

a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
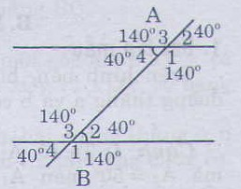
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ
a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:

c) Ta có: 
cho tam giác ABC có số đo các góc A,B tỉ lệ nghịch với các số 2;3 và số đo các góc B,C tỷ lệ thuận với 1;2. tìm số đo các góc đó
Áp dụng tc dtsbn:
\(2\widehat{A}=3\widehat{B};\dfrac{\widehat{B}}{1}=\dfrac{\widehat{C}}{2}\Rightarrow\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2};\dfrac{\widehat{B}}{1}=\dfrac{\widehat{C}}{2}\\ \Rightarrow\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+2+4}=\dfrac{180^0}{9}=20^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=60^0\\\widehat{B}=40^0\\\widehat{C}=80^0\end{matrix}\right.\)
Tìm một đa giác mà tổng số đo các góc trong bằng tổng số đo các góc ngoài
Ta có: (n - 2).1800 = 3600. Tìm được n = 4
Vậy đa giác cần tìm là tứ giác lồi
Cho tam giác ABC có số đo các góc A, B tỷ lệ nghịch với các số 2;3 và số đo các góc B,C tỷ lệ thuận với 1;2. Tìm số đo các góc của tam giác đó
Quan sát hình 5.
a) Tìm các góc kề với \(\widehat {tOz}\)
b) Tìm số đo của góc kề bù với \(\widehat {mOn}\).
c) Tìm số đo của \(\widehat {nOy}\)
d) Tìm số đo của góc kề bù với \(\widehat {tOz}\).
a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)