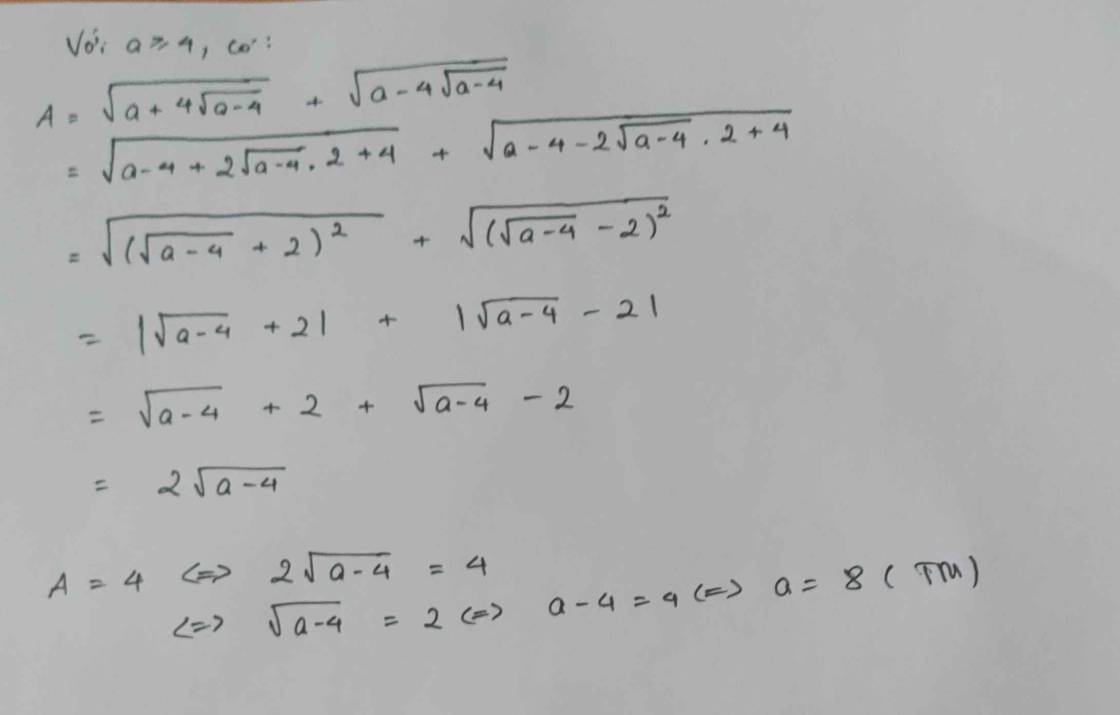A=[4;7] và B=(3m-2;dương vô cực)
tìm các giá trị của m để tập A là con của tập B
MQ
Những câu hỏi liên quan
1) rút gọn A, tìm a để A=4
\(A=\sqrt{a+4\sqrt{a-4}}+\sqrt{a-4\sqrt{a-4}}\) với a >=4
cho A =a-b/b-c + a+b / a-b và B= a^4 - b^4 / a^4 + b^4 +a^4 + b^4/ a^4 - b^4
tính B theo A a,b khác 0
a x 4 + c x a+a x 4 + c x a+a x 4 + c x a+a x 4 + c x a+a x 4 + c x a+a x 4 + c x a+a x 4 + c x a+a x 4 + c x a.Hỏi c = gì?
Cho a^2 \(\ne\)b^2 và M =\(\frac{a+b}{a-b}+\frac{a-b}{a+b}.TínhN=\frac{a^4+b^4}{a^4-b^4}+\frac{a^4-b^4}{a^4+b^4}theoM\)
Với 4 < a < 8. Rút gọn \(G=\sqrt{a+4\sqrt{a-4}}+\sqrt{a-4\sqrt{a-4}}\)
\(G=\sqrt{a-4+4\sqrt{a-4}+4}+\sqrt{a-4-4\sqrt{a-4}+4}\)
\(=\sqrt{\left(\sqrt{a-4}+2\right)^2}+\sqrt{\left(\sqrt{a-4}-2\right)^2}\)
\(=\sqrt{a-4}+2+\sqrt{a-4}-2=2\sqrt{a-4}\)
\(G = \sqrt{a + 4 \sqrt{a – 4}} + \sqrt{a – 4\sqrt{a – 4}} \) \(= \sqrt{a – 4 + 4 + 4\sqrt{a – 4}} + \sqrt{a – 4 + 4 – 4\sqrt{a – 4}}\)
\(= \sqrt{\sqrt{a - 4}^2 + 2^2 + 4\sqrt{a – 4}} + \sqrt{\sqrt{a - 4}^2 + 2^2 - 4\sqrt{a – 4}}\)
\(= \sqrt{(\sqrt{(a – 4)} + 2)^2} + \sqrt{(\sqrt{(a – 4)} - 2)^2}\)
\(= \sqrt{a – 4} + 2 +|\sqrt{a – 4} – 2|\)
+) Với \(4 < a < 8 ⇔ 0 < a – 4 < 4 ⇔ \sqrt{0} < \sqrt{a – 4} < \sqrt{4} ⇔ 0 <\sqrt{a – 4} < 2 \)
Do đó, ta có: \(G = \sqrt{a – 4} + 2 + 2 - \sqrt{a – 4} \) (vì \(2 > \sqrt{a – 4}\))
\(=4\)
➤Với \(4 < a < 8 \) thì \(G = 4 \)
Đúng 4
Bình luận (1)
1 like cho Ng.Hữu Minh và nhiều like cho H.Việt Tân.
Đúng 3
Bình luận (0)
A=(a^4+4+2a^2)(a^4-4)(a^4+4-2a^2) và B=a^12-2012^0
So sánh A và B
Cho \(C=\frac{a+b}{a-b}+\frac{a-b}{a+b}\) ; \(D=\frac{a^4+b^4}{a^4-b^4}+\frac{a^4-b^4}{a^4+b^4}\)
Tính D theo C
Cho a+b+c=0 CMR
a) a^4+b^4+c^4=2(a^2b^2+b^2c^2+c^2a^2)
b) a^4+b^4+c^4= 2(ab+bc+ca)^2
c) a^4+b^4+c^4= 1/2(a^2+b^2+c^2)^2
cho 2 số thực a,b thỏa mãn a2 # b2
Đặt A=(a+b) /(a-b) + (a-b)/(a+b). tính B =( a4 + b4)/(a4 - b4) + (a4 - b4) /(a4 + b4) theo A
Chia cả tử và mẫu của các phân số cho a khác 0 ta được:
\(A=\frac{a+b}{a-b}+\frac{a-b}{a+b}=\frac{\frac{a}{b}+1}{\frac{a}{b}-1}+\frac{\frac{a}{b}-1}{\frac{a}{b}+1}=\frac{\left(\frac{a}{b}+1\right)^2+\left(\frac{a}{b}-1\right)^2}{\left(\frac{a}{b}-1\right)\left(\frac{a}{b}+1\right)}=\frac{2.\left(\frac{a}{b}\right)^2+2}{\left(\frac{a}{b}\right)^2-1}\)
\(\Rightarrow A.\left(\frac{a}{b}\right)^2-A=2.\left(\frac{a}{b}\right)^2+2\Rightarrow A.\left(\frac{a}{b}\right)^2-2.\left(\frac{a}{b}\right)^2=A+2\)
\(\Rightarrow\left(A-2\right).\left(\frac{a}{b}\right)^2=A+2\Rightarrow\left(\frac{a}{b}\right)^2=\frac{A+2}{A-2}\)
ta có: \(B=\frac{\left(\frac{a}{b}\right)^4+1}{\left(\frac{a}{b}\right)^4-1}+\frac{\left(\frac{a}{b}\right)^4-1}{\left(\frac{a}{b}\right)^4+1}\)
\(\Rightarrow B=\frac{\left(\frac{A+2}{A-2}\right)^2+1}{\left(\frac{A+2}{A-2}\right)^2-1}+\frac{\left(\frac{A+2}{A-2}\right)^2-1}{\left(\frac{A+2}{A-2}\right)^2+1}=\frac{\left(A+2\right)^2+\left(A-2\right)^2}{\left(A+2\right)^2-\left(A-2\right)^2}+\frac{\left(A+2\right)^2-\left(A-2\right)^2}{\left(A+2\right)^2+\left(A-2\right)^2}\)
\(\Rightarrow B=\frac{2.A^2+8}{8.A}+\frac{8.A}{2.A^2+8}=\frac{\left(2A^2+8\right)^2+64.A^2}{8.A\left(2A^2+8\right)}=\frac{\left(A^2+4\right)^2+16.A^2}{4.A\left(A^2+4\right)}\)
Đúng 0
Bình luận (0)
Chia cả tử và mẫu của các phân số cho a khác 0 ta được:
$A=\frac{a+b}{a-b}+\frac{a-b}{a+b}=\frac{\frac{a}{b}+1}{\frac{a}{b}-1}+\frac{\frac{a}{b}-1}{\frac{a}{b}+1}=\frac{\left(\frac{a}{b}+1\right)^2+\left(\frac{a}{b}-1\right)^2}{\left(\frac{a}{b}-1\right)\left(\frac{a}{b}+1\right)}=\frac{2.\left(\frac{a}{b}\right)^2+2}{\left(\frac{a}{b}\right)^2-1}$A=a+ba−b +a−ba+b =ab +1ab −1 +ab −1ab +1 =(ab +1)2+(ab −1)2(ab −1)(ab +1) =2.(ab )2+2(ab )2−1
$\Rightarrow A.\left(\frac{a}{b}\right)^2-A=2.\left(\frac{a}{b}\right)^2+2\Rightarrow A.\left(\frac{a}{b}\right)^2-2.\left(\frac{a}{b}\right)^2=A+2$⇒A.(ab )2−A=2.(ab )2+2⇒A.(ab )2−2.(ab )2=A+2
$\Rightarrow\left(A-2\right).\left(\frac{a}{b}\right)^2=A+2\Rightarrow\left(\frac{a}{b}\right)^2=\frac{A+2}{A-2}$⇒(A−2).(ab )2=A+2⇒(ab )2=A+2A−2
ta có: $B=\frac{\left(\frac{a}{b}\right)^4+1}{\left(\frac{a}{b}\right)^4-1}+\frac{\left(\frac{a}{b}\right)^4-1}{\left(\frac{a}{b}\right)^4+1}$B=(ab )4+1(ab )4−1 +(ab )4−1(ab )4+1
$\Rightarrow B=\frac{\left(\frac{A+2}{A-2}\right)^2+1}{\left(\frac{A+2}{A-2}\right)^2-1}+\frac{\left(\frac{A+2}{A-2}\right)^2-1}{\left(\frac{A+2}{A-2}\right)^2+1}=\frac{\left(A+2\right)^2+\left(A-2\right)^2}{\left(A+2\right)^2-\left(A-2\right)^2}+\frac{\left(A+2\right)^2-\left(A-2\right)^2}{\left(A+2\right)^2+\left(A-2\right)^2}$⇒B=(A+2A−2 )2+1(A+2A−2 )2−1 +(A+2A−2 )2−1(A+2A−2 )2+1 =(A+2)2+(A−2)2(A+2)2−(A−2)2 +(A+2)2−(A−2)2(A+2)2+(A−2)2
$\Rightarrow B=\frac{2.A^2+8}{8.A}+\frac{8.A}{2.A^2+8}=\frac{\left(2A^2+8\right)^2+64.A^2}{8.A\left(2A^2+8\right)}=\frac{\left(A^2+4\right)^2+16.A^2}{4.A\left(A^2+4\right)}$⇒B=2.A2+88.A +8.A2.A2+8 =(2A2+8)2+64.A28.A(2A2+8) =(A2+4)2+16.A24.A(A2+4)
Đúng 0
Bình luận (0)
Cho 2 số thực a,b thỏa mãn a^2 khác b^2.
Đặt A=\(\frac{a+b}{a-b}+\frac{a-b}{a+b}\) . Tính B=\(\frac{a^4+b^4}{a^4-b^4}+\frac{a^4-b^4}{a^4+b^4}\) theo A.