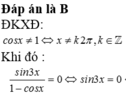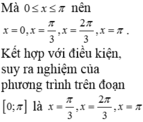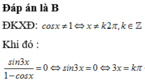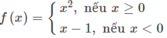trên đoạn [0;2023] có bao nhiêu giá trị nguyên của tham số a sao cho lim(\(\sqrt{9n^2+10n}-a.n\))=-\(\infty\)
NS
Những câu hỏi liên quan
Số nghiệm của phương trình sin x = 0 trên đoạn [ 0 ; π ] là:
A. 1
B. 2
C. 0
D. Vô số
Số nghiệm của phương trình sin 3 x 1 - cos x = 0 trên đoạn 0 ; π
A. 4
B. 2
C. 3
D. Vô số
Tìm GTLN, GTNN của hàm số:
a, \(y=Cosx\) trên đoạn \([-\dfrac{\pi}{2};\dfrac{\pi}{2}]\)
b, \(y=Sinx\) trên đoạn \([-\dfrac{\pi}{2};0]\)
a, Đồ thị hàm số \(y=cosx\): \(\left(A=\left(-\dfrac{\pi}{2};0\right);B=\left(\dfrac{\pi}{2};0\right)\right)\)
Dựa vào đồ thị ta có \(\left\{{}\begin{matrix}y_{min}=0\\y_{max}=1\end{matrix}\right.\)
b, Đồ thị hàm số \(y=sinx\): \(\left(A=\left(-\dfrac{\pi}{2};-1\right);A=\left(\dfrac{\pi}{2};1\right)\right)\)
Đúng 1
Bình luận (2)
Số nghiệm của phương trìn sin 3 x 1 - cos x = 0 h trên đoạn [0;ᴨ] là
A. 4
B. 2
C. 3
D. vô số
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Đúng 0
Bình luận (0)
Cho hàm số
f
x
liên tục, không âm trên đoạn
0
;
π
2
, thỏa mãn
f
0
3
và
f...
Đọc tiếp
Cho hàm số f x liên tục, không âm trên đoạn 0 ; π 2 , thỏa mãn f 0 = 3 và f x . f ' x = cos x . 1 + f 2 x , ∀ x ∈ 0 ; π 2 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f x trên đoạn π 6 ; π 2 .
A. m = 21 2 , M = 2 2 .
B. m = 5 2 , M = 3
C. m = 5 2 , M = 3 .
D. m = 3 , M = 2 2 .
Cho đg tròn (0) đg kinh BC và điểm A € (0) trên tia đối của tia AB lấy đoạn AD=AC trên tia đối của tia AC lấy đoạn AE=AB.C/m OA vuông góc vs DE
Kéo dài OA cắt DE tại M
\(\Delta ABC\)nội tiếp ( O ) đường kính BC nên vuông tại A \(\Rightarrow\Delta ADE\)vuông tại A
Xét \(\Delta ABC\)và \(\Delta ADE\)có :
\(\widehat{BAC}=\widehat{EAD}=90^o\)
\(AB=AE\)
\(AD=AC\)
\(\Rightarrow\Delta ABC=\Delta AED\left(c.g.c\right)\)
\(\Rightarrow\widehat{E_1}=\widehat{B_1}\)
OA = OC nên \(\Delta OAC\)cân tại O \(\Rightarrow\widehat{A_2}=\widehat{C_1}\)
Mặt khác : \(\widehat{A_1}=\widehat{A_2}\)( hai góc đối đỉnh )
\(\Rightarrow\widehat{E_1}+\widehat{A_1}=\widehat{B_1}+\widehat{C_1}=90^o\Rightarrow\widehat{EMO}=90^o\)
Vậy OA \(\perp\)DE
Trên một đoạn mạch xoay chiều, hệ số công suất bằng 0 (cosφ = 0), khi
A. đoạn mạch có điện trở bằng không.
B. đoạn mạch không có tụ điện.
C. đoạn mạch không có cuộn cảm
D. đoạn mạch chỉ chứa điện trở thuần
Đáp án A
Hệ số công suất của đoạn mạch RLC không phân nhánh: 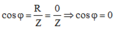
Đúng 0
Bình luận (0)
Cho hàm số
f
x
liên tục, không âm trên đoạn
0
;
π
2
thỏa mãn
f
0
3
và
f
x
....
Đọc tiếp
Cho hàm số f x liên tục, không âm trên đoạn 0 ; π 2 thỏa mãn f 0 = 3 và f x . f ' x = cos x . 1 + f 2 x , ∀ x ∈ 0 ; π 2 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f x trên đoạn π 6 ; π 2
A. m = 21 2 , M = 2 2
B. m = 5 2 , M = 3
C. m = 5 2 , M = 3
D. m = 3 , M = 2 2
Chọn đáp án A
Từ giả thiết
![]()
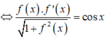

![]()
![]()
Suy ra
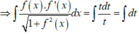
![]()
Từ (1) và (2) suy ra 1 + f 2 x = sin x + C
Thay x = 0 vào ta được:
![]()
do f 0 = 3
Suy ra
![]()
![]()
![]()
do hàm số f x liên tục, không âm trên 0 ; π 2
Đặt t = sin x
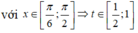
Xét hàm số g t = t 2 + 4 t + 3 trên 1 2 ; 1
Ta có

⇒ Hàm số g t đồng biến trên 1 2 ; 1
Khi đó
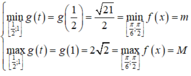
Đúng 0
Bình luận (0)