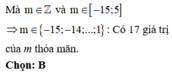Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017]để hàm số y = (m − 2)x + 2m đồng biến trên R.
A. 2014
B. 2016
C. Vô số
D. 2015
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017]để hàm số y = ( m 2 − 4)x + 2m đồng biến trên R.
A. 4030
B. 4034
C. Vô số
D. 2015
Cho hàm số y = m sin x + 1 cos x + 1 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5;5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 5
C. 4
D. 3
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1.
![]()
![]()
![]()
![]()
có bao nhiêu giá trị nguyên của tham số m thuộc đoạn -5,5 để pt (m\(^2\)-4)x=m(m-2) có nghiệm duy nhất
Lời giải:
Để $(m^2-4)x=m(m-2)$ có nghiệm duy nhất thì $m^2-4\neq 0$
$\Leftrightarrow (m-2)(m+2)\neq 0$
$\Leftrightarrow m\neq \pm 2$
Mà $m$ nguyên và $m\in [-5;5]$ nên $m\in\left\{-5; -4; -3; -1; 0; 1;3;4;5\right\}$
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để hàm số y=(m-2)x+2 đồng biến trên R?
A. 2017
B. 2015
C. Vô số
D. 2016
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để hàm số y = (m-2)x + 2 đồng biến trên ℝ ?
A. 2017
B. 2015
C. Vô số
D. 2016
Chọn D
Phương pháp:
Sử dụng: Hàm số y = ax+b đồng biến ⇔ a > 0, từ đó kết hợp điều kiện đề bài để tìm các giá trị của m.
Cách giải:
Hàm số y = (m-2)x + 2 đồng biến trên ℝ ⇔ m - 2 > 0 ⇔ m > 2
Mà ![]()
![]() => có 2016 giá trị nguyên của m thỏa mãn đề bài.
=> có 2016 giá trị nguyên của m thỏa mãn đề bài.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình m x 2 - m x + 1 = 0 có nghiệm.
A. 17
B. 18
C. 20
D. 21
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 5 ; 5 để phương trình e x = m x + 1 có nghiệm duy nhất?
A. 5
B. 6
C. 7
D. 10
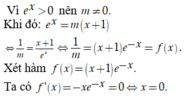

Dựa vào BBT, ta thấy phương trình có nghiệm duy nhất
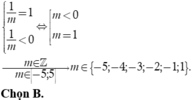
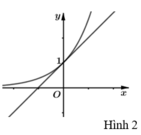
Ta có y = e x là hàm đồng biến trên ℝ và y = e x > 0 với mọi x ∈ ℝ có đồ thị (C)(xem hình 1).
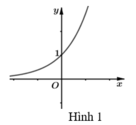
Do đó:
= Nếu m < 0 thì y = m(x+1) là hàm số nghịch biến trên ℝ , có đồ thị là một đường thẳng luôn qua điểm (-1;0) nên luôn cắt đồ thị (C): y = e x tại duy nhất một điểm.
= Nếu m = 0 phương trình vô nghiệm (do y = e x > 0).
= Nếu m > 0 để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng
![]() là tiếp tuyến của (C) (như hình 2)
là tiếp tuyến của (C) (như hình 2)
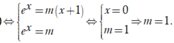
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn − 15 ; 5 để phương trình 4 x + m 2 x + 2 m − 4 = 0 có nghiệm?
A. 18.
B. 17.
C. 20.
D. 19.

+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.
Cách giải: