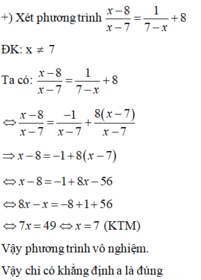Tìm nghiệm của phương trình sau trong đoạn [0;2π]
5(sinx+\(\frac{cos3x+sin3x}{1+sin2x}\))=cos2x+3
TN
Những câu hỏi liên quan
Số điểm biểu diễn các nghiệm của phương trình sin3x - cos3x + căn3 0 trên đường tròn lượng giác? Nghiệm của phương trình sinx căn2 Phương trình sin2x (căn3)/2 có bao nhiêu nghiệm trên đoạn [-pi; 2pi] Trong mặt phẳng tọa độ Oxy Tìm ảnh đường tròn C: x² + y² - 4y + 6y - 12. Qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép vị tự tâm O tỉ số k 2
Đọc tiếp
Số điểm biểu diễn các nghiệm của phương trình sin3x - cos3x + căn3 = 0 trên đường tròn lượng giác?
Nghiệm của phương trình sinx = căn2 Phương trình sin2x = (căn3)/2 có bao nhiêu nghiệm trên đoạn [-pi; 2pi]
Trong mặt phẳng tọa độ Oxy Tìm ảnh đường tròn C: x² + y² - 4y + 6y - 12. Qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép vị tự tâm O tỉ số k = 2
Dùng hệ thức vi-ét để tìm nghiệm x 2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x 2 - 13x + m=0 có nghiệm x 1 =12,5
Theo hệ thức Vi-ét ta có: x 1 + x 2 =13
Suy ra 12,5 + x 2 = 13 ⇔ x 2 = 0,5
Cũng theo hệ thức Vi-ét ta có: x 1 x 2 = m
Suy ra: m = 12,5.0,5 ⇔ m =6,25
Vậy với m = 6,25 thì phương trình x 2 -13x + m = 0 có hai nghiệm
x 1 =12,5 , x 2 =0,5
Đúng 0
Bình luận (0)
Dùng hệ thức vi-ét để tìm nghiệm x 2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x 2 +mx -35 =0 có nghiệm x 1 =7
Theo hệ thức Vi-ét ta có: x 1 x 2 =-35
Suy ra 7 x 2 =-35 ⇔ x 2 =-5
Cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =-m
Suy ra: m=-7 +5 ⇔ m =-2
Vậy với m =-2 thì phương trình x 2 + mx - 35 = 0 có hai nghiệm x 1 =7, x 2 =-5
Đúng 0
Bình luận (0)
Dùng hệ thức vi-ét để tìm nghiệm
x
2
của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình
x
2
+ 3x –
m
2
+ 3m 0 có nghiệm
x
1
-2
Đọc tiếp
Dùng hệ thức vi-ét để tìm nghiệm x 2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x 2 + 3x – m 2 + 3m =0 có nghiệm x 1 = -2
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - 3/4
Suy ra: -2 + x 2 = - 3/4 ⇔ x 2 = -3/4 + 2 = 5/4
Cũng theo hệ thức Vi-ét ta có: x 1 x 2 = (- m 2 +3m)/4
Suy ra: -2. 5/4 = (- m 2 +3m)/4 ⇔ m 2 -3m -10 =0
∆ = - 3 2 -4.1.(-10) =9+40 =49
∆ = 49 =7
m 1 =(3 +7)/(2.1) =5 ; m 2 =(3 -7)/(2.1) =-2
Vậy với m =5 hoặc m = -2 thì phương trình 4 x 2 +3x – m 2 +3m = 0 có hai nghiệm x 1 =-2 , x 2 =5/4
Đúng 0
Bình luận (0)
Dùng hệ thức vi-ét để tìm nghiệm x 2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x 2 - 2(m -3)x + 5 =0 có nghiệm x 1 =1/3
Theo hệ thức Vi-ét ta có: x 1 x 2 =5/3
Suy ra: 1/3 . x 2 = 5/3 ⇔ x 2 =5/3 : 1/3 =5/3 .3=5
cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =[2(m -3)]/3
Suy ra: 1/3 +5 = [2(m -3)]/3 ⇔ 2(m -3) =16 ⇔ m-3=8 ⇔ m=11
Vậy với m = 11 thì phương trình 3 x 2 -2(m -3)x +5 =0 có hai nghiệm x 1 = 1/3 , x 2 = 5
Đúng 0
Bình luận (0)
Cho phương trình : mx2 - 2x - 4m - 1 = 0
a. Chứng mình rằng với mọi giá trị của m ≠ 0 phương trình đã cho có hai nghiệm phân biệt.
b. Tìm giá trị của m để -1 là một nghiệm của phương trình. Sau đó tìm nghiệm còn lại.
a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1
= 
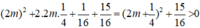với mọi m.
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0
⇔ m + 2 - 4m = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.
Đúng 0
Bình luận (0)
Tìm số nghiệm của phương trình sin cosx = 0 trên đoạn x∈[0;2π].
A. 0
B. 1
C. 2
D. Vô số
Tìm nghiệm của phương trình sau:
A. x = 1/2 B. x = 1
C. x = 0 D. phương trình vô nghiệm
Điều kiện của phương trình:
4x – 3 ≥ 0 ⇒ x ≥ 3/4;
-2x + 1 ≥0 ⇒ x ≤ 1/2.
Không có giá trị nào của x thỏa mãn hai điều kiện này nên phương trình vô nghiệm.
Đáp án: D
Đúng 0
Bình luận (0)
Tìm số nghiệm thuộc đoạn
2
π
;
4
π
của phương trình
sin
2
x
cos
x
+
1
0.
A. 5 B. 6 C. 3 D. 4
Đọc tiếp
Tìm số nghiệm thuộc đoạn 2 π ; 4 π của phương trình sin 2 x cos x + 1 = 0.
A. 5
B. 6
C. 3
D. 4
Đáp án D
P T ⇔ cos x + 1 ≠ 0 sin 2 x = 0 ⇔ cos x ≠ − 1 2 x = k π ⇔ x ≠ π + k 2 π x = k π 2 ⇒ x = k 2 π x = π 2 + k π k ∈ ℤ .
x ∈ 2 π ; 4 π ⇒ 2 π ≤ k 2 π ≤ 4 π 2 π ≤ π 2 + k π ≤ 4 π ⇔ 1 ≤ k ≤ 2 3 2 ≤ k ≤ 7 2
Suy ra PT có 4 nghiệm thuộc đoạn 2 π ; 4 π .
Đúng 0
Bình luận (0)
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
