Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−\(\dfrac{\pi}{2}\);2π]
để hàm số y=cotx
nhận giá trị dương
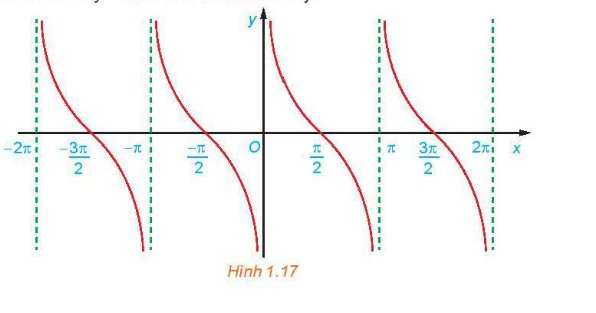
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−π2;2π] để hàm số y=cotx nhận giá trị dương.

cot x>0
=>\(x\in\left(0;\dfrac{pi}{2}\right)\cup\left(pi;\dfrac{3}{2}pi\right)\)
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn [−π;\(\dfrac{3\pi}{2}\)] để hàm số y=tanx
nhận giá trị âm.
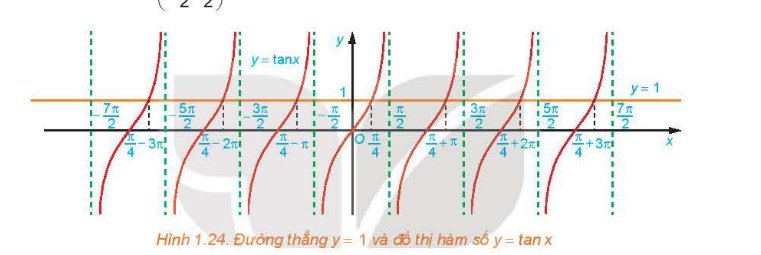
tan x<0
=>\(x\in\left(-\dfrac{pi}{2};0\right)\cup\left(\dfrac{pi}{2};pi\right)\)
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.
Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
Cho đồ thị của hàm số y= ( m-\(\dfrac{1}{2}\)) x ( vs m là hằng số ) đi qua điểm A(2;4)
a) Xác định m
b) Vẽ đồ thị của hàm số đã cho vs giá trị m tìm đc ở câu a
c) Bằng phép tính , tìm trên đồ thị hàm số vs giá trị của m ở điểm a trên điểm có tung độ là -2
Cho đồ thị của hàm số y = (m - ![]() )x (với m là hằng số,
)x (với m là hằng số,![]() ) đi qua điểm A(2;4).
) đi qua điểm A(2;4).
a) Xác định m.
b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a.Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2.
Cho đồ thị của hàm số y = (m - )x (với m là hằng số,) đi qua điểm A(2;4). a) Xác định m; b) Vẽ đồ thị của hàm số đã cho với giá trị m tìm được ở câu a.Tìm trên đồ thị hàm số trên điểm có tung độ bằng 2.
Vẽ đồ thị hàm số \(y = \cos x\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.
Vẽ đồ thị:
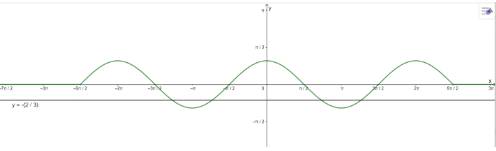
\(3\cos x + 2 = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 4 nghiệm
Cho hàm số y= f(x) xác định và liên tục trên đoạn [-1;3] có đồ thị như hình vẽ sau.
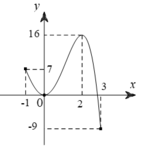
Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = f ( x ) + m trên đoạn [-1;3] bằng 2018?
A. 2.
B. 4.
C. 6
D. 0.