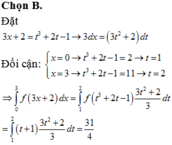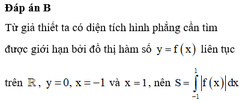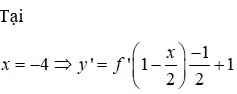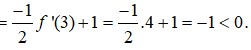cho h/s y = f(x) liên tục trên R sao cho gtln cùa f(x) trên [-1;2] bằng 3. Xét g(x) = f(3x - 1) + m. Tìm m để gtln của g(x) bằng -10 trên doan [0;1]
HH
Những câu hỏi liên quan
cho hàm số y = f(x) liên tục trên R sao cho maxf(x) = 3 trên [-1;2] Xét g(x) = f(3x-1) + m Tìm m để maxg(x) trên [0;1 bằng -10
Cho hàm số \(y=f\left(x\right)\) liên tục trên R, có đạo hàm \(f'\left(x\right)=x\left(x-1\right)^2\left(x-2\right)\) . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho hàm số \(y=f\left(\dfrac{x+2}{x+m}\right)\) đồng biến trên khoảng \(\left(10;+\infty\right)\) . Tính tổng các phần tử của S.
NT
19 tháng 4 2022 lúc 22:45
Cho h/s y = f(x) liên tục trên R ; f'(x) = 0 có đúng 2 no x=1 ; x=2 . H/s g(x) = \(f\left(x^2+4x-m\right)\) . Có bn g/t nguyên của m \(\in\left[-2021;2022\right]\) để p/t g'(x) = 0 có nhiều no nhất ?
Ta có : \(f'\left(1\right)=f'\left(2\right)=0\) ; \(g\left(x\right)=f\left(x^2+4x-m\right)\) \(\Rightarrow g'\left(x\right)=\left(2x+4\right)f'\left(x^2+4x-m\right)\)
g'(x) = 0 \(\Leftrightarrow\left[{}\begin{matrix}x=-2\\f'\left(x^2+4x-m\right)=0\left(1\right)\end{matrix}\right.\)
g'(x) có nhiều no nhất \(\Leftrightarrow\left(1\right)\) có nhiều no nhất \(\Leftrightarrow x^2+4x-m=1\) và \(x^2+4x-m=2\) đều có 2 no
\(x^2+4x-m=1\) có 2 no \(\Leftrightarrow\Delta'=m+5>0\Leftrightarrow m>-5\)
\(x^2+4x-m=2\) có 2 no \(\Leftrightarrow m>-6\)
Vậy m > -5
Mà m \(\in\left[-2021;2022\right]\) nên m \(\in\left[-4;2022\right]\)
=> Có : 2023 + 4 = 2027 giá trị nguyên của m t/m
Đúng 2
Bình luận (0)
Cho hàm số yf(x) liên tục và xác định trên R sao cho
f
(
x
)
x
3
+
2
x
-
1
)
x
+
1
. Giá trị của tích phân
∫
0
2
f
(
3
x
+
2
)
d
x
tương ứng bằng A. 12 B. 31/4...
Đọc tiếp
Cho hàm số y=f(x) liên tục và xác định trên R sao cho f ( x ) = x 3 + 2 x - 1 ) = x + 1 . Giá trị của tích phân ∫ 0 2 f ( 3 x + 2 ) d x tương ứng bằng
A. 12
B. 31/4
C. 15/2
D. -24/5
Cho hàm số y f(x) liên tục trên R và thỏa mãn f(-1) 0 f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y f(x), y 0 và x 1. Mệnh đề nào sau đây là đúng? A. S
∫
-
1
0
f
(
x
)
d
x
+
∫
0
1
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0 và x = 1. Mệnh đề nào sau đây là đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 f ( x ) d x
B. S = ∫ - 1 1 f ( x ) d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
H24
28 tháng 4 2022 lúc 22:36
Hãy tìm tất cả các h/s f(x) x/đ ; liên tục trên R ; lấy giá trị trong R và t/m các đ/k : \(f\left(x-y\right)f\left(y-z\right)f\left(z-x\right)+8=0\) \(\forall x;y;z\in R\)
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
(
1
-
x
)
2
(
x
+
1
)
3
(
3
-
x
)
. Hàm số
y
f
(
x
)
đồng biến trên khoảng nào dưới đây
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = ( 1 - x ) 2 ( x + 1 ) 3 ( 3 - x ) . Hàm số y = f ( x ) đồng biến trên khoảng nào dưới đây
Cho hàm số yf(x) có đạo hàm liên tục trên R. Biết f(1)e và
(
x
+
2
)
f
(
x
)
x
f
(
x
)
-
x
3
, với mọi x thuộc R. Tính f(2). A.
4
e
2
-
4
e
+
4
B.
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4
Cho hàm số yf(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số yf(x) được cho như hình vẽ bên. Hàm số
y
f
(
1
-
x
2
)
+
x
nghịch biến trên khoảng A. (-4;-2) B. (2;4) C. (0;2) D. (-2;0)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng
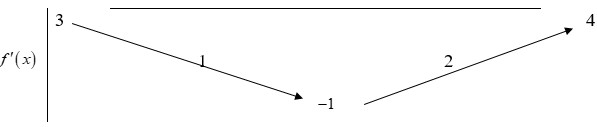
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
