Trong không gian với hệ tọa độ Oxy, cho hai điểm A(2;3;1), B(0;1;2). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. (P): 2x+2y-z=0
B. (P): 2x+2y-z-9=0
C. (P): 2x+4y+3z-19=0
D. (P): 2x+4y+3z-10=0.
Trong không gian với hệ tọa độ Oxy, cho đường thẳng ∆ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxy, cho đường thẳng △ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất
A. M(5;2;-4)
B. M(-1;-1;-1)
C. M(1;0;-2)
D. M(3;1;-3)
Trong không gian với hệ tọa độ Descartes Oxy cho hai điểm A(1, a) và B( -a, 2). Diện tích tam giác OAB có thể đạt giá trị nhỏ nhất bằng
A. 0
B. 1
C. 2
D. 3
Chọn B.
Đường thẳng AB có phương trình là
![]()
Khoảng cách từ O tới đường thẳng AB bằng
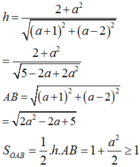
Diện tích tam giác OAB đạt giá trị nhỏ nhất bằng 1 khi a = 0
Trong không gian với hệ trục tọa độ Oxy, cho hai điểm A ( − 2 ; 1 ; 1 ) và B ( 0 ; − 1 ; 1 ) . Viết phương trình mặt cầu đường kính AB
A. ( x + 1 ) 2 + y 2 + ( z − 1 ) 2 = 8.
B. ( x + 1 ) 2 + y 2 + ( z − 1 ) 2 = 2.
C. ( x − 1 ) 2 + y 2 + ( z + 1 ) 2 = 2.
D. ( x − 1 ) 2 + y 2 + ( z + 1 ) 2 = 8.
Đáp án B.
Gọi I là trung điểm của AB thì I(–1;0;1). Ta có A B = 2 2 . Suy ra mặt cầu (S) đường kính AB sẽ có tâm là I, bán kính R = A B 2 = 2 .
Phương trình mặt cầu (S) là: x + 1 2 + y 2 + z − 1 2 = 2.
Trong không gian với hệ trục tọa độ Oxy, viết phương trình tham số của đường thẳng đi qua hai điểm A ( 1 ; 2 ; − 3 ) , B ( 2 ; − 3 ; 1 )
A. x = 1 + t y = 2 − 5 t z = − 3 − 2 t .
B. x = 2 + t y = − 3 + 5 t z = 1 + 4 t .
C. x = 1 + t y = 2 − 5 t z = 3 + 4 t .
D. x = 3 − t y = − 8 + 5 t z = 5 − 4 t .
Đáp án D.
Ta có A B → = ( 1 ; − 5 ; 4 ) nên vectơ chỉ phương của đường thẳng AB là u A B → = ( 1 ; − 5 ; 4 )
Trong không gian với hệ tọa độ Oxy, cho hai điểm A 3 ; 2 ; 0 , B 1 ; 0 ; - 4 . Mặt cầu nhận AB làm đường kính có phương trình là
A. x 2 + y 2 + z 2 - 4 x - 2 y + 4 z - 15 = 0
B. x 2 + y 2 + z 2 + 4 x + 2 y - 4 z - 15 = 0
C. x 2 + y 2 + z 2 - 4 x - 2 y + 4 z + 3 = 0
D. x 2 + y 2 + z 2 + 4 x + 2 y - 4 z + 3 = 0
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất
A. M(-2;-1;0)
B. M(-2;-1;0)
C. M(2;-1;0)
D. M(2;1;0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(2;0;4)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(0;-1;0).
Đáp án C
Do chiếu xuống (Oxy) nên z=0 và x,y giữ nguyên.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;2;3). Khi đó điểm M' đối xứng với M qua mặt phẳng (Oxy) có tọa độ là
A. M'(1;2;3)
B. M'(-1;-2;3)
C. M'(-1;2;-3)
D. M'(1;-2;3)