a. Lập pt của đtròn(C) tâm I(4;2) tiếp xúc với đg thẳng 3x+4y+5=0
b. Viết pt tiếp tuyến của đtròn(C) song song với trục Oy
Cho nửa đtròn tâm O đường kính AB = 2R . trên nữa mặt phẳng bờ AB chứa nữa đường tròn vẽ tiếp tuyến Ax , By . Một tiếp tuyến qua M cắt Ax tại c cắt by tại E và AB tại F . CM thuộc nửa đtròn(khac A và B) chứng minh .
a)CE = CA +BE
b)AC.BE= R2
c) Gọi i là tâm của đtròn đkính CE . chứng minh ab là tiếp tuyến của đường tròn tâm i
d) Kẻ MH vuông góc với AB . chứng minh HA/HB = FA/FB
cho tam giác ABC nhọn, các đường cao BD,CE cắt nhau tại H. Gọi I là tiếp điểm của AH .
CMR : a) 4 điểm A,D,H cùng thuộc đường tròn tâm I
b) 4 điểm B,D,E,C cùng thuộc 1 đtròn
(Chỉ mang t/c minh họa)
1/ Ta có I là trung điểm của AH (gt)
=> AI = AH = 1/2 AH (1)
BD _|_ AC tại D và H thuộc BC (gt)
=> △ABD vuông tại A
Xét △AHD vuông tại D có I là trung điểm của AH
=> DI = 1/2 AH (2)
Cmtt ta có : EI = 1/2 AH (3)
Từ (1)(2)(3) => AI = HI = DI = EI
=> 4 điểm A,D,H,E cùng thuộc 1 đtròn(I)
2/ Ta có : BD _|_ AC tại D (gt)
=> ^BDC = 90o
Cmtt ta có : ^BEC = 90o
=> ^BDC = ^BEC = 90o
=> 4 điểm B,E,D,C cùng thuộc 1 đtròn
Cho đường tròn ( O; R ) , điểm A cố định nằm trên đường tròn , kẻ tiếp tuyến d qua A với ( O ) . Trên d lấy điểm M ( M khác A ) , từ M kẻ tiếp tuyến thứ 2 là MB với ( O ) ( B là tiếp điểm )
a, CM 4 điểm A , O , B , M cùng nằm trên 1 đt
b , Đoạn OM cắt đtròn ( O ) tại I . Chứng minh BI là phân giác của góc MAB . Từ đó suy ra I là tâm của đtròn nội tiếp tam giác MAB
c, gọi H là trực tâm của tam giác MAB . Điểm H chạy trên đường nào khi M chạy trên d
cho đtròn tâm O, đường kính AB=2R. lấy điểm c trên đtròn. Trên cùng 1 nửa mặt phẳng bờ AB chứa điểm C dựng 2 tia Ax và By cùng vuông góc với AB. Qua điểm C dựng tiếp tuyến với đtròn cắt tia Ax và By lần lượt tại M và N.
a.cm 4 điểm M, C, O, A cùng nằm trên 1 đtròn
b. cm góc CMO bằng góc CAO.
c. cm BC.MN=2R.ON
(gợi ý;: cm 2 tam giác vuông đồng dạng , 2R là đường kính của đtròn.)
d. khi AM = \(R\sqrt{3}\) hãy tính tỉ số diện tích của tm giác ACB và tam giác MON.
a) Xét tứ giác AOCM có
\(\widehat{MAO}\) và \(\widehat{MCO}\) là hai góc đối
\(\widehat{MAO}+\widehat{MCO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AOCM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
nên A,O,C,M cùng nằm trên một đường tròn(đpcm)
cho đường tròn (O;4,5 cm) và đường tròn (O';2 cm) tiếp xúc ngoài tại A.Gọi CD là tiếp tuyến chung ngoài (C thuộc đtròn tâm O, D thuộc đtròn tâm O'). Tiếp tuyến chung trong của 2 đtròn cắt CD tại M.
a. TÍnh số đo góc OMO' và góc CAD
b. Tính độ dài CD
c. Chứng tỏ đường tròn tâm I dường kính OO' tiếp xúc với CD tại M.
và các bãn vẽ hình giùm mình luôn nha mình ko bít vẽ nên ko làm dc, cám ơn các bạn, bài này trong đề cương học kì mai cô giáo kiểm rồi các bạn giúp mình nha
Trong mp toạ đọ Oxy, cho ∆ ABC biết A(-1,2), B(1,2), C(2,-3). Lập pt đường tròn (T) ngoại tiếp ∆ABC. Tìm toạ độ tâm (I) của đtron (T)
\(PT\left(T\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\)
\(\left\{{}\begin{matrix}A\left(-1;2\right)\in\left(T\right)\\B\left(1;2\right)\in\left(T\right)\\C\left(2;-3\right)\in\left(T\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2+2^2+2a-4b+c=0\\1^2+2^2-2a-4b+c=0\\2^2+\left(-3\right)^2-4a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-4b+c=-5\\-2a-4b+c=-5\\-4a+6b+c=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-\dfrac{4}{5}\\c=-\dfrac{41}{5}\end{matrix}\right.\)
\(\Rightarrow\)Tâm \(I\left(0;-\dfrac{4}{5}\right)\)
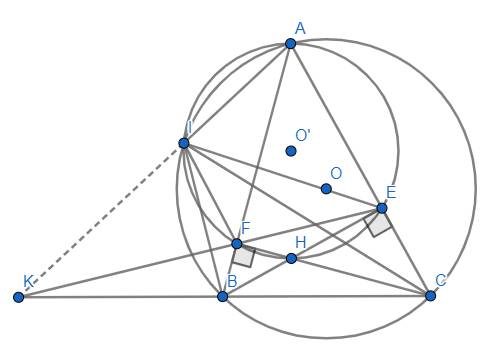
Cho tam giác ABC có 3 góc nhọn( AB < AC ) và nội tiếp đtròn (O). Gọi BE,CF là các đường cao và H là trực tâm của tam giác ABC. CM a.Đường tròn ngoại tiếp tứ giác AEHF và đtròn O tại điểm thứ hai I ( I ko trùng A).CM IBC đồng dạng IFE b.Hai đường thẳng BC và EF cắt nhau tại k. Cm 3 điểm A,I,K thẳng hàng Giúp tớ voi ạ
(a) Gọi \(O'\) là tâm đường tròn ngoại tiếp tứ giác \(AIFE.\)
Ta có : \(\hat{IEF}=\hat{IAF}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{IEF}=\hat{IAB}.\)
Mà : \(\hat{IAB}=\hat{ICB}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(IB\)).
Do đó, \(\hat{IEF}=\hat{ICB}.\)
Ta cũng có : \(\hat{FIE}=\hat{FAE}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{FIE}=\hat{BAC}.\)
Mà : \(\hat{BAC}=\hat{BIC}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(BC\)).
Do đó, \(\hat{FIE}=\hat{BIC}.\)
Xét \(\Delta IBC,\Delta IFE:\left\{{}\begin{matrix}\hat{ICB}=\hat{IEF}\left(cmt\right)\\\hat{BIC}=\hat{FIE}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta IBE\sim\Delta IFE\left(g.g\right)\) (đpcm).
(b) Mình tạm thời chưa nghĩ ra nhé:)
Cho đtròn tâm O có bán kính R. Vẽ hai đường kính AC và BD vuông góc với nhau. Lấy điểm M là trung điểm của OB. Tia AM cắt đtròn tại E (E khác A).
a) C/m OMEC nội tiếp.
b)Tính AM.AE+CD\(^2\) theo R.
c)Gọi N là trung điểm của CD. C/m MN//CE.
d)Tính diện tích tam giác ANE theo R.
a) Vì AB là đường kính \(\Rightarrow\angle AEC=90\) mà \(\angle MOC=90\Rightarrow OMEC\) nội tiếp
b) Xét \(\Delta AMO\) và \(\Delta ACE:\) Ta có: \(\left\{{}\begin{matrix}\angle AOM=\angle AEC=90\\\angle CAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AM}{AO}=\dfrac{AC}{AE}\Rightarrow AM.AE=AO.AC=2R^2\)
Ta có: \(CD^2=CO^2+OD^2=2R^2\Rightarrow AM.AE+CD^2=4R^2\)
c) \(\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AM}{AO}=\dfrac{1}{2}=\dfrac{AD}{DN}\)
Xét \(\Delta ADN\) và \(\Delta AEC:\) Ta có: \(\left\{{}\begin{matrix}\angle ADN=\angle AEC=90\\\dfrac{AC}{AE}=\dfrac{AD}{DN}\end{matrix}\right.\)
\(\Rightarrow\Delta ADN\sim\Delta AEC\Rightarrow\angle AND=\angle ACE=\angle AMO\Rightarrow AMND\) nội tiếp
mà \(\angle ADN=90\Rightarrow\angle AMN=90\Rightarrow NM\bot AE\) mà \(CE\bot AE\)
\(\Rightarrow MN\parallel CE\)
d) Ta có: \(AM=\sqrt{AO^2+OM^2}=\dfrac{\sqrt{5}}{2}R\)
\(\Delta AMO\sim\Delta ACE\Rightarrow\dfrac{AE}{AC}=\dfrac{AO}{AM}=\dfrac{R}{\dfrac{\sqrt{5}}{2}R}=\dfrac{2}{\sqrt{5}}\)
\(\Rightarrow AE=\dfrac{4}{\sqrt{5}}R\)
AMND nt \(\Rightarrow\angle MAN=\angle MDN=\angle MDA=\angle MNA\Rightarrow\Delta MAN\) vuông cân tại M \(\Rightarrow MN=MA=\dfrac{\sqrt{5}}{2}R\)
Ta có: \(S_{ANE}=\dfrac{1}{2}NM.AE=\dfrac{1}{2}.\dfrac{\sqrt{5}}{2}R.\dfrac{4}{\sqrt{5}}R=R^2\)
về ý tưởng cơ bản là vậy,còn mình có tính toán gì sai thì bạn sửa nhé
cho điểm A(-1;2) đt \(\Delta\) 2x - y-1 =0 và đtròn ( c) (x-1)\(^2\) + (y-2)\(^2\)=9
tìm tọa độ giao điểm a1 là ảnh của a qua Đox
tìm tọa độ điểm a2 là ảnh của a qua Đoy
viết pt đt \(\Delta^,\) là ảnh của \(\Delta\) qua Đox
viết pt đtron ( c\(^,\)) là ảnh của (c) qua Đoy
giải nhanh giúp mình với
a: Tọa độ A1 là ảnh của A qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_{A_1}=x_A=-1\\y_{A_1}=-y_A=-2\end{matrix}\right.\)
Vậy: \(A_1\left(-1;-2\right)\)
b: Tọa độ A2 là ảnh của A qua phép đối xứng trục Oy là:
\(\left\{{}\begin{matrix}x_{A_2}=-x_A=1\\y_{A_2}=y_A=2\end{matrix}\right.\)
Vậy: \(A_2\left(1;2\right)\)
c: Tọa độ giao điểm B của (Δ) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-y-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Vậy: B(1/2;0)
Vì B thuộc Ox nên phép đối xứng qua trục Ox biến B thành chính nó
Lấy C(1;1) thuộc (d)
Tọa độ D là ảnh của C qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_D=x_C=1\\y_D=-y_C=-1\end{matrix}\right.\)
Vậy: D(1;-1)
Do đó: Δ' là phương trình đường thẳng đi qua hai điểm B(1/2;0); D(1;-1)
\(\overrightarrow{BD}=\left(\dfrac{1}{2};-1\right)=\left(1;-2\right)\)
=>VTPT là (2;1)
Phương trình Δ' là:
\(2\left(x-1\right)+1\left(y+1\right)=0\)
=>2x-2+y+1=0
=>2x+y-1=0