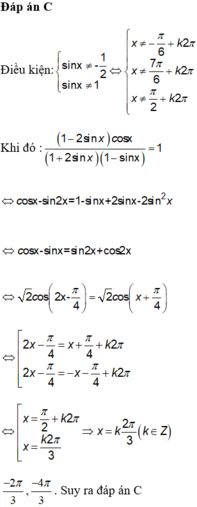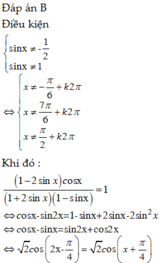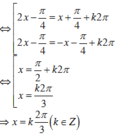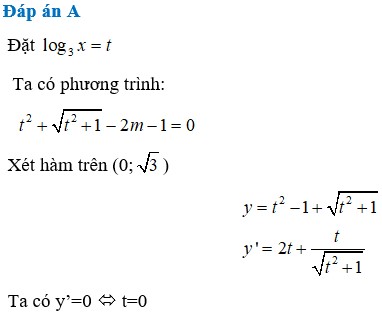Tìm tổng tất cả các nghiệm thuộc đoạn \(\left[0;10\Pi\right]\) của phương trình : \(sin^22x+3sin2x+2=0\) .
A . \(\frac{105\Pi}{2}\)
B . \(\frac{105\Pi}{4}\)
C . \(\frac{297\Pi}{4}\)
D . \(\frac{299\Pi}{4}\)
Trình bày bài giải chi tiết rồi ms chọn đáp án nha các bạn .