tìm hàm số bậc hai y=ax2 + bx + c có đồ thị của nó có đỉnh I(-2;1) và cắt đưởng thẳng y=x-1 tại 1 điểm trên trục tung
TS
Những câu hỏi liên quan
Câu 12. Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
A. y = x 2 − 3x + 2. B. y = 2x 2 − 4x + 3. C. y = x 2 − 2x. D. y = x 2 + 2x
xác định hàm số bậc hai ax2+bx+c biết rằng đồ thị hàm số là parabol đi qua điểm B<0,4> và có đỉnh I <1,5>
Theo đề, ta có: c=4
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)
Đúng 0
Bình luận (0)
câu 1: xác định hàm số bậc hai y = \(2x^2\)+ bx +c , biết rằng đồ thị của nó có đỉnh là I ( -1 ; 0)
câu 2 : xác định phương trình (P) y=\(ax^2\)+ bx+c đi qua ba điểm A ( 0:-1) B ( 1:-1) C ( -1:1)?
Câu 1:
Đỉnh của đths \((\frac{-b}{2a}, \frac{4ac-b^2}{4a})=(\frac{-b}{4},\frac{8c-b^2}{8})=(-1;0)\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{-b}{4}=-1\\ \frac{8c-b^2}{8}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=4\\ 8c=b^2=16\end{matrix}\right.\Leftrightarrow b=4; c=2\)
Đúng 2
Bình luận (1)
Câu 2:
ĐTHS đi qua 3 điểm $A, B,C$ nên:
\(\left\{\begin{matrix}
-1=a.0^2+b.0+c\\
-1=a.1^2+b.1+c\\
1=a(-1)^2+b(-1)+c\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
c=-1\\
a+b+c=-1\\
a-b+c=1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} c=-1\\ a=1\\ b=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
2
+
b
x
+
c
a
≠
0
có đồ thị (P). Biết đồ thị của hàm số có đỉnh I (1;1) và đi qua điểm A(2;3). Tính tổng
S
a
2
+
b...
Đọc tiếp
Cho hàm số y = a x 2 + b x + c a ≠ 0 có đồ thị (P). Biết đồ thị của hàm số có đỉnh I (1;1) và đi qua điểm A(2;3). Tính tổng S = a 2 + b 2 + c 2 .
A. 3.
B. 4.
C. 29.
D. 1.
Cho hàm số y ax2 + bx + c có đồ thị (P). Tọa độ đỉnh của (P) là: A. B. C. D.
Đọc tiếp
Cho hàm số y = ax2 + bx + c có đồ thị (P). Tọa độ đỉnh của (P) là:
A. 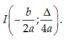
B. 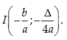
C. 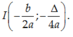
D. 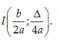
Hàm số bậc hai
y
a
x
2
-
2
x
+
c
có đồ thị với đỉnh I(2; -1) là A. y (
x
2
/ 2) - 2x + 1 B. y (
x
2
/ 2) - 2x + 3 C. y
x
2
- 2x - 1 D. y 2
x...
Đọc tiếp
Hàm số bậc hai y = a x 2 - 2 x + c có đồ thị với đỉnh I(2; -1) là
A. y = ( x 2 / 2) - 2x + 1
B. y = ( x 2 / 2) - 2x + 3
C. y = x 2 - 2x - 1
D. y = 2 x 2 - 2x - 5
Đáp án: A (kiểm tra hoành độ đỉnh x = (-b)/2a; sai đó kiểm tra tung độ đỉnh)
Đúng 0
Bình luận (0)
cho đồ thị hàm số y=ax2+bx+4 có đỉnh là điểm I(1,-2). Tính a+3b
A.20
B.-18
C.-3-
D.25
Lời giải:
Đỉnh của đths là $(\frac{-b}{2a}, 4-\frac{b^2}{4a})=(1,-2)$
$\Rightarrow \frac{-b}{2a}=1; 4-\frac{b^2}{4a}=-2$
$\Rightarrow -b=2a; b^2=24a$
$\Rightarrow a=0$ hoặc $a=6$
Nếu $a=0$ thì $b=-2a=0$. Khi đó đths $y=4$ là đường thẳng song song với trục hoành, không có đỉnh I(1,-2)$
Nếu $a=6$ thì $b=-2a=-12$. Khi đó: $a+3b=6+3(-12)=-30$
Đúng 3
Bình luận (0)
Dùng công thức c - ax² = y cho toạ độ đỉnh ta có :
4 - a.1² = -2
=> a = 6
Thế vào b = -2a ,Ta có :
b = -12
=> a + 3b = 6 - 3.(-12) = -30
Đúng 0
Bình luận (0)
Nếu hàm số y ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là: A.a0; b0; c 0 B.a 0; b0; c 0 C. a0; b0; c 0 D. A0; b0; c 0
Đọc tiếp
Nếu hàm số y= ax2+ bx+c có đồ thị như sau thì dấu các hệ số của nó là:
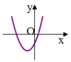
A.a>0; b>0; c> 0
B.a> 0; b>0; c< 0
C. a>0; b<0; c> 0
D. A>0; b<0; c< 0
+ Nhận xét đồ thị hướng lên nên a> 0.
+ Giao với Oy tại (0; c) mà điểm đó nằm phía dưới trục hoành nên c<0.
+ Mặt khác; vì a>0 và Đỉnh I nằm bên trái trục hoành nên b>0.
Chọn B.
Đúng 0
Bình luận (0)
Nếu hàm số
y
a
x
2
+
b
x
+
x
có
a
0
,
b
0
,
c
0
thì đồ thị của nó có dạng nào trong các hình sau?
Đọc tiếp
Nếu hàm số y = a x 2 + b x + x có a > 0 , b < 0 , c < 0 thì đồ thị của nó có dạng nào trong các hình sau?

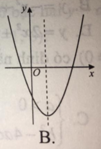
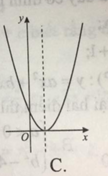
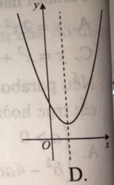
Ta có: x = − b 2 a > 0 nên trục đối xứng nằm bên phải trục Oy
Đồ thị cắt trục tung tại điểm (0; c) nằm dưới trục hoành ( vì c < 0).
Do đó, đồ thị B là đồ thị của hàm số đã cho.
Đáp án B
Đúng 0
Bình luận (0)




