Đáp án D

Đỉnh của parabol là \(\frac{-\Delta}{4a}\) ta có

\(\left\{{}\begin{matrix}\frac{-\Delta}{4a}=-25\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\24a+c=0\\2a+b=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4a^2-4ac=100a\\24a+c=0\\b=-2a\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a-c=25\\24a+c=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-24\end{matrix}\right.\)

\(\Rightarrow y=x^2-2x-24\)

em mới lớp 8 nên làm đc mỗi câu 2 :(

2. pt có nghiệm <=> Δ' ≥ 0

<=> ( -m - 2 )² - ( m² + 4m - 12 ) ≥ 0

<=> m² + 4m + 4 - m² - 4m + 12 ≥ 0

<=> 16 ≥ 0 ( đúng với mọi m )

Vậy với mọi m thì pt có nghiệm

Khi đó theo hệ thức Viète ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+4\\x_1x_2=\dfrac{c}{a}=m^2+4m-12\end{matrix}\right.\)

| x₁ + x₂ | ≤ 6

<=> | x₁ + x₂ |² ≤ 36

<=> ( x₁ + x₂ )² ≤ 36

<=> x₁² + 2x₁x₂ + x₂² ≤ 36

<=> ( x₁ + x₂ )² - 2x₁x₂ ≤ 36

<=> ( 2m + 4 )² - 2( m² + 4m - 12 ) ≤ 36

<=> 4m² + 16m + 16 - 2m² - 8m + 24 ≤ 36

<=> 2m² + 8m - 4 ≤ 0

<=> m² + 4m - 2 ≤ 0

<=> ( m + 2 )² - 6 ≤ 0

<=> ( m + 2 - √6 )( m + 2 + √6 ) ≤ 0 

<=> -2 - √6 ≤ m ≤ - 2 + √6

Vậy ...

Theođề, ta có hệ:

a*0+b=-2 và a+b=0

=>b=-2; a=-b=2

Vì đồ thị hàm số y=ax+b cắt hai điểm \(\left(0;3\right)\) và \(\left(-2;0\right)\) nên ta có hệ phương trình:

\(\left\{{}\begin{matrix}b=3\\a\cdot\left(-2\right)+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\-2a=-b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=3\end{matrix}\right.\)

Bài 1:

a: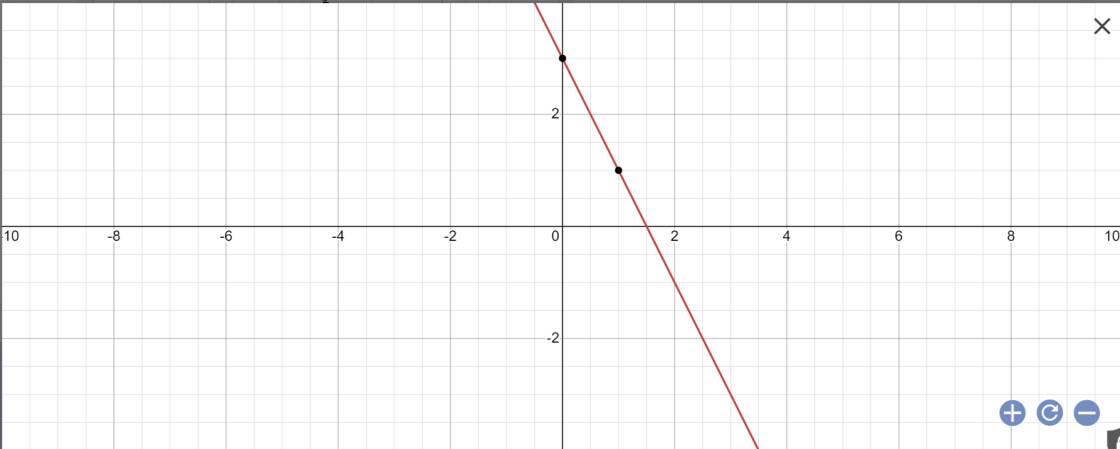 

b: Vì (d')//(d) nên \(\left\{{}\begin{matrix}a=-2\\b< >3\end{matrix}\right.\)

vậy: (d'): y=-2x+b

Thay x=2 và y=0 vào (d'), ta được:

\(b-2\cdot2=0\)

=>b-4=0

=>b=4

Vậy: (d'): y=-2x+4

Vì đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng 2 nên b=2

Vì đồ thị hàm số y = ax + 2 cắt trục hoành tại điểm có hoành độ bằng -2 nên tung độ của giao điểm bằng 0, ta có:

0 = a.(-2) + 2 ⇔ 2a = 2 ⇔ a = 1

Vậy hàm số đã cho là y = x + 2.

\(\left(d\right)//\left(d_1\right):y=\dfrac{2}{3}x+1\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b\ne1\end{matrix}\right.\)

Ta có: (d) cắt trục hoành tại điểm có hoành độ là 3

\(\Rightarrow A\left(3;0\right)\in\left(d\right)\Leftrightarrow y_A=ax_A+b\)

\(\Leftrightarrow0=3.\dfrac{2}{3}+b\Leftrightarrow b=-2\)

Vậy \(\left(d\right):y=\dfrac{2}{3}x-2\)

Sửa đề: cắt trục tung tại điểm có tung độ bằng -3

Thay x=0 và y=-3 vào (P), ta được:

\(a\cdot0^2+b\cdot0+c=-3\)

=>0+0+c=-3

=>c=-3

vậy: (P): \(y=ax^2+bx-3\)

Tọa độ đỉnh là I(-1;-4) nên ta có:

\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4\cdot a\cdot\left(-3\right)}{4a}=-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=2a\\\dfrac{b^2+12a}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\left(2a\right)^2+12a=16a\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=2a\\4a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\4a\left(a-1\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=2a\\\left[{}\begin{matrix}a=0\left(loại\right)\\a-1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)