Cho dãy số (un) : \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};....\) Số hạng tổng quát của dãy số (un) là :
A. \(u_n=\frac{n-1}{n}\)
B. \(u_n=\frac{n}{n+1}\)
C. \(u_n=\frac{n^2-n}{n+1}\)
D. \(u_n=\frac{n+1}{n+2}\)
Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.
Cho dãy số (un) xác định như sau: u1= 2; un+1 - un - 2 + 2(4un+1 - \(\sqrt{4u_n+1}\)) = 0, ∀n∈ N*. Tìm số hạng tổng quát un của dãy số trên
Cho hai dãy số u n và v n . Biết | u n – 2 | ≤ v n với mọi n và l i m v n = 0 . Có kết luận gì về giới hạn của dãy số u n ?
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
Cho dãy số u n với u n = 1 / n .
Biểu diễn u n dưới dạng khai triển: 1 ; 1 2 ; 1 3 ; . . . . ; 1 100 ; . . .
Biểu diễn u n trên trục số (h.46):

a) Nhận xét xem khoảng cách từ u n tới 0 thay đổi như thế nào khi n trở nên rất lớn.
b) Bắt đầu từ số hạng u n nào của dãy số thì khoảng cách từ u n đến 0 nhỏ hơn 0,01? 0,001?
a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01
Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001
Cho hai dãy số ( u n ) và ( v n ) . Chứng minh rằng nếu lim v n = 0 v à | u n | ≥ v n với mọi n thì l i m u n = 0
l i m v n = 0 ⇒ | v n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi (1)
Vì | u n | ≤ v n v à v n ≤ | v n | với mọi n, nên | u n | ≤ | v n | với mọi n. (2)
Từ (1) và (2) suy ra | u n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi, nghĩa là l i m u n = 0
Cho dãy số (un) được xác định như sau: u 1 = 1 u n = 3 u n - 1 + 1 2 u n - 1 - 2 , n ≥ 2 Viết 4 số hạng đầu của dãy và chứng minh rằng un > 0, ∀ n
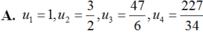
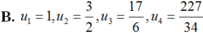
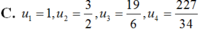
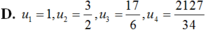
Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: 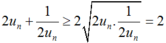
Nên 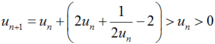 .
.
Cho dãy số ( u n ) thỏa mãn log u 1 2 + u 2 2 + 10 - log 2 u 1 + 6 u 2 = 0 và u n + 2 + u n = 2 u n + 1 + 1 với mọi n∈ N*. Giá trị nhỏ nhất của n để u n >5050 bằng
A. 101.
B. 102.
C. 100.
D. 99.
Cho dãy số u n thỏa mãn log u 1 2 + u 2 2 + 10 - log 2 u 1 + 6 u 2 = 0 v à u n + 2 + u n = 2 u n + 1 + 1 với mọi n ∈ ℕ * . Giá trị nhỏ nhất của n để u n > 5050 bằng
A. 101
B. 102
C. 100
D. 99
Cho dãy số u n xác định bởi u 1 = 0 và u n + 1 = u n + 4 n + 3 với ∀ n ≥ 2 . Biết rằng dãy số thỏa mãn l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + u 2 2018 n = a 2019 + b c với a, b, c là các số nguyên dương và b < 2019. Tính giá trị của S = a + b - c
A. S = -1
B. S = 0
C. S = 2017
D. S = 2018
Đáp án B
Ta có
![]()
Với mỗi
![]() và
và ![]()
Ta có
![]()
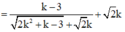
Khi đó
![]()
Và
![]()

Vậy
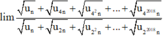
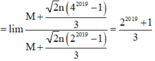 .
.
Biết rằng dãy số ( u n ) có giới hạn là 0. Giải thích vì sao dãy số ( v n ) với v n = | u n | cũng có giới hạn là 0. Chiều ngược lại có đúng không?
Vì ( u n ) có giới hạn là 0 nên | u n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Mặt khác, | v n | = | | u n | | = | u n | . Do đó, | v n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy ( v n ) có giới hạn là 0.