Tính chiều cao của tháp ở bên kia sông biết BC = 50m; góc AHB= 32° và góc AHC= 46° và ba điểm B,C,H thẳng hàng ( kết quả làm tròn đến chữ số thập phân thứ nhất )
KT
Những câu hỏi liên quan
tính chiều cao của tháp ở bên kia sông
tính chiều cao CH của tháp ở bên kia sông, biết AB=25m, góc HAC= 32 °, góc HBC= 43 ° và ba điểm A,B,H thẳng hàng.( làm tròn đến chữ số thập phân thứ nhất ).
mong mọi người giúp ạ :Tính chiều cao CH của tháp ở bên kia sông biết AB = 25cm; 0 0 43 ˆ 32 ; ˆ HAC = HBC = và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
Một chiếc đò đang ở điểm A muốn băng qua sông theo đường AH vuông góc với bờ bên kia nhưng bị nước cuốn đi nên tấp vào bờ bên kia ở điểm B cách H 50m (BH = 50m). Tìm chiều rộng con sông (AH) và quãng đường đò đã đi (AB).
Xem chi tiết
Giúp mik zoi
chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)
Đúng 0
Bình luận (1)
Kim tự tháp Kê-ốp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231 m. Tính cạnh bên và diện tích một mặt bên của kim tự tháp.
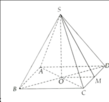
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h 1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được ∠DA1C1 49o và ∠DB1C1 35o. Tính chiều cao CD của tháp đó.
Đọc tiếp
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được ∠DA1C1 = 49o và ∠DB1C1 = 35o. Tính chiều cao CD của tháp đó.

Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
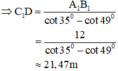
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.
Đúng 0
Bình luận (0)
Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia người ta nhìn thấy đỉnh tháp với góc nâng 600. Từ một điểm khác cách điểm ban đầu 20 m người ta cũng nhìn thấy đỉnh tháp với góc nâng 300 (Hình minh họa). Tính chiều cao của tháp và bề rộng của sông
Đọc tiếp
Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia người ta nhìn thấy đỉnh tháp với góc nâng 600. Từ một điểm khác cách điểm ban đầu 20 m người ta cũng nhìn thấy đỉnh tháp với góc nâng 300 (Hình minh họa). Tính chiều cao của tháp và bề rộng của sông
Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)
Đúng 0
Bình luận (0)
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không? Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB x theo BC a, B’C’ a’; BB’ h.
Đọc tiếp
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB =x theo BC =a, B’C’ = a’; BB’ = h.
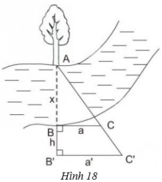
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 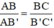 (hệ quả định lý Talet)
(hệ quả định lý Talet)
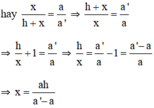
Đúng 0
Bình luận (0)
Kim tự tháp Kheops - Ai Cập có dạng hình mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m
a) Tính chiều cao h của kim tự tháp ( làm tròn đến mét)
b) Cho biết thể tích của hình chóp được tính theo công thức V 1/3S.h, trong đó S là diện tích mặt đáy, h là chiều cao hình chóp. Tính theo m3 thể tích của kim tự tháp này (làm tròn đến hàng nghìn)
Đọc tiếp
Kim tự tháp Kheops - Ai Cập có dạng hình mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m
a) Tính chiều cao h của kim tự tháp ( làm tròn đến mét)
b) Cho biết thể tích của hình chóp được tính theo công thức V = 1/3S.h, trong đó S là diện tích mặt đáy, h là chiều cao hình chóp. Tính theo m3 thể tích của kim tự tháp này (làm tròn đến hàng nghìn)