Vật m = 32 kg được treo vào tường bỡi dây xích BC và thanh AB. Thanh AB gắn vào tường bỡi bản lề A; góc . Bỏ qua khối lượng của thanh. Lấy g = 10m/s2. Tính phản lực của tường tác dụng lên thanh AB .
dạ em cần lời giải chi tiết ạ ! Em cảm ơn >
Cho một vật có khối lượng m = 6kg được treo vào tường bởi dây BC và thanh AB. Thanh AB gắn vào tường bằng bản lề A, ta có AB = 30cm và BC = 60cm. Tìm các lực tác dụng lên thanh AB, bỏ qua khối lượng thanh
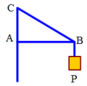
A. 20 3
B. 10 3
C. 20 2
D. 5 3
Một ngọn đèn khối lượng m 1 = 4 k g được treo vào tường bởi dây BC và thanh cứng AB. Thanh AB khối lượng của thanh AB có khối lượng m 2 = 2 k g được gắn vào tường ở bản lề tại A. Cho α = 30 ° ; lấy g = 10 m / s 2 . Tìm lực căng của dây treo.
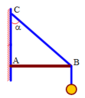
A. 57,7N
B. 30,6N
C. 40,0N
D. 60,0N
Một ngọn đèn khối lượng m1 = 4kg dược treo vào tường bởi dây BC và thanh cứng AB. Thanh AB khối lượng của thanh AB có khối lượng m2 = 2 kg được gắn vào tường ở bản lề tại A
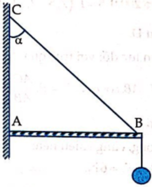
Cho = 30°; lấy g = 10m/s2. Tìm lực căng của dây treo
A. 57,7N
B. 30,6N
C. 40,0N
D. 60,0N
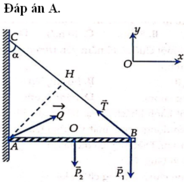
Quy tắc mômen đối với trục quay qua A:
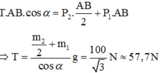
Một ngọn đèn khối lượng m 1 = 4 k g được treo vào tường bởi dây BC và thanh cứng AB. Thanh AB khối lượng của thanh AB có khối lượng m 2 = 2 k g được gắn vào tường ở bản lề tại A. Cho α = 30 ° ; lấy g = 10 m / s 2 . Tìm góc tạo bởi phàn lực của tường tác dụng lên thanh AB tại A và thanh AB.
A. 30 °
B. 0 °
C. 60 °
D. 180 °
Một ngọn đèn có khối lượng 2kg được treo vào tường bởi sợi dây BC và thanh AB. Thanh AB gắn với tường nhờ vào bản lề A, với AC và BC tạo với nha một góc 60 0 .Tìm lực căng của dây tác dụng lên thanh AB nếu bỏ qua khối lượng thanh. Lấy g=10 m / s 2
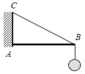
A. 40N
B. 20N
C. 15N
D. 10N
Đáp án A
P A B = T . A H = T . A B . sin 30 0 ⇒ T = P sin 30 0 = 20 0 , 5 = 40 N
Cho một vật có khối lượng m = 6kg được treo vào tường bởi dây BC và thanh AB. Thanh AB gắn vào tường bằng bản lề A, ta có AB = 30cm và BC = 60cm
1. Tìm các lực tác dụng lên thanh AB trong hai trường hợp sau:
a. Bỏ qua khối lượng thanh.
b. Khối lượng thanh AB là 3kg.
2. Khi tăng góc A C B ^ thì lực căng dây BC thay đổi như thế nào ?
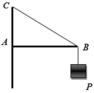
1. Ta có
P = m g = 6.10 = 60 ( k g ) S i n A C B ^ = A B B C = 30 60 ⇒ A C B ^ = 30 0 ⇒ A B C ^ = 60 0
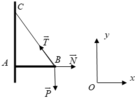
a, Phản lực N → có hướng A B → . Theo điều kiện cân bằng:
T → + P → + N → = 0 → ; T = P = 40 N
Chiếu lên Oy
T . cos 30 0 − P = 0 ⇒ T = P cos 30 0 = 60 3 2 = 40 3 ( N )
Chiếu lên Ox
⇒ T . sin 30 0 − N = 0 ⇒ N = 40 3 . 1 2 = 20 3 ( N )
b, Phản lực có phương nằm trong góc. Cân bằng đối với trục quay ở A:
M T → = M P → 1 + M P → 2 ⇒ T . A B sin 60 0 = P 1 . A B 2 + P 2 . A B ⇒ T = 3.10.0 , 5 + 60 3 2 = 50 3 ( N )
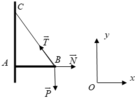
Phương trình cân bằng lực:
T → + P → 1 + P → 2 + N → = 0 →
Chiếu theo Ox
N x = T x = T cos 60 0 = 50. 3 2 = 25 3 ( N )
Chiếu theo Oy
N y + T y − P 1 − P 2 = 0 ⇒ N y = 30 + 60 − 50 3 . 3 2 = 15 ( N )
Vậy
N = N x 2 + N y 2 = 15 2 + ( 25 3 ) 2 = 10 21 ( N ) { N x = T x = T cos 60 0 = T 2 = 50 3 2 = 25 3 ( N ) N y = P + P ' − T ' cos α = ( m + m ' ) g − T ' cos α
2.Theo ý a ta có: T = m g cos A C B ^
Theo ý b ta có T = P 1 2 + P 2 cos A C B ^
Vậy khi tăng A C B ^ thì lực căng T tăng
Một ngọn đèn có khối lượng 2kg được treo vào tường bởi sợi dây BC và thanh AB. Thanh AB gắn với tường nhờ vào bản lề A, với AC và BC tạo với nhau một góc 60 ° . Tìm lực căng của dây tác dụng lên thanh AB nếu bỏ qua khối lượng thanh. Lấy g = 10 m / s 2
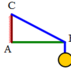
A. 40N
B. 20N
C. 15N
D. 10N
Một thanh BC nhẹ, gắn vào tường bởi bản lề C, đầu B treo vật có khối lượng m = 4kg và được giữ cân bằng nhờ dây treo AB. Cho AB = 30cm, AC = 40cm. Xác định lực tác dụng lên BC
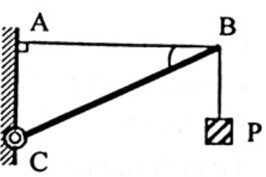
A. 50 N
B. 50 3 N
C. 30 N
D. 30 2 N
Đặt thanh AB có khối lượng không đáng kể nằm ngang, đầu A gắn vào tường nhừ một bản lề, đàu B nối với tường bằng dây BC. Treo vào B một vật có khối lượng 3kg, cho AB=40cm, AC= 30cm. Tính lực căng trên dây BC và lực nén lên thanh AB. Lấy g = 10 m / s 2 .
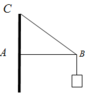
Ta có P = mg = 3.10=30 (N)
Biểu diễn các lực như hình vẽ
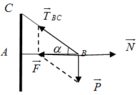
Theo điều kiện cân bằng
T → B C + N → + P → = 0 ⇒ F → + N → = 0
⇒ F → ↑ ↓ N → F = N
Xét tam giác ABC ta có
S i n α = A C B C = A C A B 2 + A C 2 = 30 30 2 + 40 2 = 3 5
C o s α = A B B C = A B A B 2 + A C 2 = 40 40 2 + 30 2 = 4 5
Theo hình biểu diễn
S i n α = P T B C ⇒ T B C = 30 3 5 = 50 ( N )
C o s α = F T B C = N T B C ⇒ N = T B C . C o s α = 50. 4 5 = 40 ( N )