Cho a,n thuộc N sao ; biết an chia hết cho 5 => chứng minh rằng a2 + 150 chia hết cho 25
DJ
Những câu hỏi liên quan
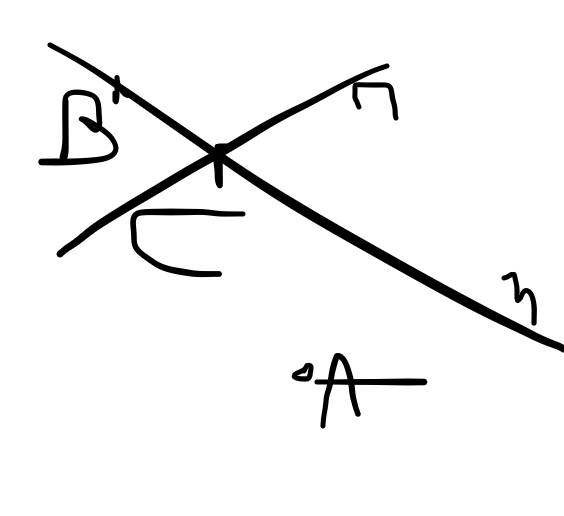
Cho hai đường thẳng m, n
a) Vẽ điểm A sao cho A không thuộc m và không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Vẽ điểm C sao cho C thuộc m và C thuộc n
Cho 2 đường thẳng m,n
a) Về điểm A sao cho A không thuộc m và A không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Về điểm C sao cho c thuộc m và C thuộc n
Cho hai đường thẳng m, n
a) Vẽ điểm A sao cho A không thuộc m và không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Vẽ điểm C sao cho C thuộc m và C thuộc n
Cho A=\(\frac{3}{n-2}\),n thuộc Z,tìm n sao cho A thuộc Z
Cho B=\(\frac{n}{n-1}\),n tuộc Z,tìm n sao cho B thuộc Z
A thuộc Z
<=> 3 chia hết cho n - 2
<=> n - 2 thuộc Ư(3) = {-3; -1; 1; 3}
<=> n thuộc {-1; 1; 3; 5}
B thuộc Z
<=> n chia hết cho n - 1
<=> n - 1 + 1 chia hết cho n - 1
<=> 1 chia hết cho n - 1
<=> n - 1 thuộc Ư(1) = {-1;1}
<=> n thuộc {0; 2}.
Đúng 0
Bình luận (0)
Bạn nào làm nhanh và đúng nhất mình sẽ đúng cho!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Tập hợp A ta có n = 3 thì ta sẽ có phân số 3/3 = 1; 1 thuộc Z
Tập hợp B ta có n= 2 thì ta đc phân số 2/1 =2; 2 thuộc Z
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a/ Tìm x thuộc N Sao cho N + 2 chia hết n - 1
b/ Tìm x thuộc N Sao cho 2n + 7 chia hết cho n+1
Viết thế này dễ nhìn nefk (n+2)/(n-1) =(n-1+3)/(n-1)
=1+3/(n-1) vì n+2 chia cho n-1 =1 dư 3/(n-1)
để n+2 chia hết cho n-1 thì 3/(n-1) là số nguyên
3/(n-1) nguyên khi (n-1) là Ước của 3
khi (n-1) ∈ {±1 ; ±3}
xét TH thôi :
n-1=1 =>n=2 (tm)
n-1=-1=>n=0 (tm)
n-1=3=>n=4 (tm)
n-1=-3=>n=-2 (loại) vì n ∈N
Vậy tại n={0;2;4) thì n+2 chia hết cho n-1
--------------------------------------...
b, (2n+7)/(n+1)=(2n+2+5)/(n+1)=[2(n+1)+5]/(...
2n+7 chia hêt cho n+1 khi 5/(n+1) là số nguyên
khi n+1 ∈ Ước của 5
khi n+1 ∈ {±1 ;±5} mà n ∈N => n ≥0 => n+1 ≥1
vậy n+1 ∈ {1;5}
Xét TH
n+1=1=>n=0 (tm)
n+1=5>n=4(tm)
Vâyj tại n={0;4) thì 2n+7 chia hêt scho n+1
--------------------------------------...
Chúc bạn học tốt
Đúng 0
Bình luận (0)
a/ N + 2 chia hết n - 1
có nghĩa là \(\frac{n+2}{n-1}\) là số nguyên
\(\frac{n+2}{n-1}=1+\frac{3}{n-1}\) muốn nguyên thì n-1 thuộc Ư(3)={-1,-3,1,3}
n-1=-1=>n=0n-1=1=>n=2n-1=-3=>n=-2n-1=3=>n=4do n thuộc N => cacsc gtri thỏa là {0,2,4}
b/ 2n + 7 chia hết cho n+1 có nghĩa là : \(\frac{2n+7}{n+1}=2+\frac{5}{n+1}\)
là số nguyên
để nguyên thì n+1 thuộc Ư(5)={1,5,-1,-5}
n+1=1=>n=0n+1=-1=>n=-2n+1=5=>n=4n+1=-5=>n=-6do n thuộc N nên : các giá trị n la : {0;4}
Đúng 0
Bình luận (0)
a) \(\frac{n+2}{n-1}\Leftrightarrow\frac{n-1+3}{n-1}=\frac{3}{n-1}\)
Để 3 chia hết cho n - 1 thì n - 1 thuộc Ư (3)
Ư (3) = {1;-1;3;-3}
=> n = {2;0;4;-2}
Mà n thuộc n nên loại 2 vậy n = {2;0;4}
b) \(\frac{2n+7}{n+1}=\frac{n+1+6.2}{n+1}=\frac{12}{n+1}\)
Để 4 chia hết n+1 thì n+1 thuộc Ư(12)
Ư (12) = {1;2;3;4;-1;-2;-3;-4;-12}
=> n thuộc N loại số âm.
n + 1 = 1 => n = 0
n + 1 = 2 => n = -1 (loại)
n + 1 = 3 => n = -2 (loại)
n + 1 = -12 => n = -13 (loại)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Viết tập hợp sau bằng cách liệt kê rồi tính số phần tử:a) A{x thuộc N sao cho 10 bé hơn x bé hơn 16}b) B{ x thuộc N sao cho 10 bé hơn hoặc bằng 20}c) C { x thuộc N sao cho 5 bé hơn x bé hơn hoặc bằng 10}d) D {x thuộc N sao cho 10 be hơn x bé hơn hoặc bằng 100} e) E{ x thuộc N sao cho 2982 bé hơn x bé hơn 2987}f) F { x thuộc N* sao cho x bé hơn 10}g) G{ x thuộc N* sao cho x bé hơn hoặc bằng 4}h) H {x thuộc N* sao cho x bé hơn hoặc bằng 100}i) I { x thuộc N sao cho 32 bé hơn hoặc bằng 2015}
Đọc tiếp
1. Viết tập hợp sau bằng cách liệt kê rồi tính số phần tử:
a) A={x thuộc N sao cho 10 bé hơn x bé hơn 16}
b) B={ x thuộc N sao cho 10 bé hơn hoặc bằng 20}
c) C= { x thuộc N sao cho 5 bé hơn x bé hơn hoặc bằng 10}
d) D= {x thuộc N sao cho 10 be hơn x bé hơn hoặc bằng 100}
e) E={ x thuộc N sao cho 2982 bé hơn x bé hơn 2987}
f) F= { x thuộc N* sao cho x bé hơn 10}
g) G={ x thuộc N* sao cho x bé hơn hoặc bằng 4}
h) H= {x thuộc N* sao cho x bé hơn hoặc bằng 100}
i) I= { x thuộc N sao cho 32 bé hơn hoặc bằng 2015}
A=11,12,13,14,15.
B=11,12,13,14,15,16,17,18,19,20.
C=6,7,8,9,10.
D=11,12,13,14,15,16,17,18,19,20,21,22,.........,98,99,100.
F=1,2,3,4,5,6,7,8,9.
G=1,2,3,4.
H=1,2,3,4,5,6,7,8,9,10,11,12,13,14,...............,98,999,100.
I=32,33,34,35,36,37,38,39,40,41,42,43,...................,2013,2014,2015
k nhé
Đúng 1
Bình luận (0)
C = { x thuộc N sao cho x = 4a +3 ; a thuộc N ; 2 \(\le a\le20\)
D= {x thuộc N sao cho x. (x-4).(2x-6)=0}
tìm n thuộc N sao cho
a) n+3/n+1 thuộc N
b)n.n+3n/n-1 thuộc N
Cho p/số:
P = 7 - n ^n - 3
a)Tìm n thuộc Z sao cho P thuộc Z.
b)Tìm n sao cho P<1
cho :
A=6n+42/6n với n thuộc Z;n khác 0
tìm n thuộc Z sao cho a thuộc Z
Ta có : \(A=\frac{6n+42}{6n}=1+\frac{42}{6n}\)
\(=1+\frac{7}{n}\)
Để \(1+\frac{7}{n}\in Z\) \(\Rightarrow\frac{7}{n}\in Z\)
\(\Rightarrow7⋮n\) \(\Rightarrow n\inƯ\left(7\right)=\left\{1;-1;7;-7\right\}\)
Vậy \(n\in\left\{1;-1;7;-7\right\}\)
Đúng 0
Bình luận (0)