Cho tam giác ABC biết góc A=90o, AB=AC; MB=MC=1/2 BC
E thuộc đoạn CM. Kẻ BK,CH vuông góc với AE
CMR MBK là tam giác vuông cân
NT
Những câu hỏi liên quan
Cho tam giác vuông ABC, góc A = 90o, góc C = 30o và đường phân giác BD (D thuộc cạnh AC).
a) Tính tỉ số AD/CD.
b) Cho biết độ dài AB = 12,5cm. Hãy tính chu vi và diện tích của tam giác ABC.
a) + Δ ABC vuông tại A, có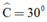 
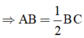
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của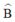 
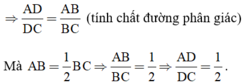
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
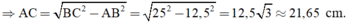
+ Chu vi tam giác ABC là:
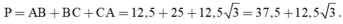
+ Diện tích tam giác ABC là:
Đúng 1
Bình luận (1)
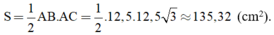
1. Cho tam giác ABC có góc A < 90o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD, AE sao cho: AD _|_ AB, AD = AB và AE _|_ AC, AE = AC. Chứng minh rằng: DC = BE và DC _|_ BE
2. Cho tam giác ABC có góc A < 90o. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD, AE sao cho: AD _|_AB, AD = AB và AE _|_ AC, AE = AC. Từ B kẻ BK _|_ CD tại K. Chứng minh rằng 3 điểm E,K,B thẳng hàng
Câu 5: Cho tam giác ABC có góc A=90o , đường cao AH. Biết BC=13cm, AB=8cm.
a. Tính độ dài các đoạn thẳng AC, AH, HB,HC.
b. Tính số đo góc ABC.
Cho tam giác ABC, gọi M là trung điểm BC. Biết AB = 6cm, AC = 10cm, AM = 4cm. Chứng minh góc MAB = 90o.
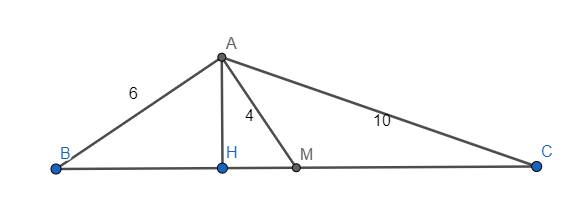
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)
Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)
Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:
\(2\left(h^2+x^2+y^2\right)=136\)
\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)
\(\Leftrightarrow x^2+16=68\)
\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)
Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)
\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm
Đúng 1
Bình luận (0)
Gọi H là điểm đối xứng với A qua M
Xét tam giác AMB và tam giác HMC có:
\(\left\{{}\begin{matrix}HM=AM\\\widehat{AMB}=\widehat{HMC}\\MB=MC\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta HMC\left(c.g.c\right)\)
\(\Rightarrow HC=AB=6cm\)
Xét tam giác HAC có:
\(AH^2+HC^2=10^2\left(8^2+6^2=10^2\right)\)
\(\Rightarrow\widehat{AHC}=90^o\)
Mà \(\Delta AMB=\Delta HMC\)
\(\Rightarrow\widehat{MAB}=\widehat{MHC}=90^o\left(đpcm\right)\)
Đúng 1
Bình luận (0)
C ho tam giác ABC có A bé hơn 90o trên nửa mặt phẳng chứa đỉnh C bờ AB kẻ AE sao cho AE vuông góc AB, AE = AB trên nửa mặt phẳng ko chứa điểm B bờ AC kẻ tia AD sao cho AD vuông góc với AC,AD=Ac. Chứng minh tam giác ABC= tam giác AED
Xét △ABC và △AED có
AB=AE(gt)
BAC =EAD( đối đỉnh)
AC=AD(gt)
Vậy △ABC=△AED(c-g-c)
Đúng 1
Bình luận (1)
Vẽ tam giác ABC có góc A = 90o, AB = AC = 3cm. Sau đó đo các góc B và C.
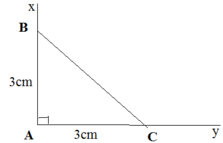
- Cách vẽ:
+ Vẽ góc xAy = 90o
+ Trên tia Ax vẽ đoạn thẳng AB = 3cm
+ Trên tia Ay vẽ đoạn thẳng AC = 3cm
+ Vẽ đoạn thẳng BC
Ta được tam giác ABC là tam giác cần vẽ
- Đo các góc B và C ta được góc B = góc C = 45º
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác DEF có AB DE,
B
^
E
^
,
A
^
D
^
90
o
. Biết AC 9cm. Độ dài DF là: A. 10 cm B. 5 cm C. 9 cm D. 7 cm
Đọc tiếp
Cho tam giác ABC và tam giác DEF có AB = DE, B ^ = E ^ , A ^ = D ^ = 90 o . Biết AC = 9cm. Độ dài DF là:
A. 10 cm
B. 5 cm
C. 9 cm
D. 7 cm
Cho tam giác ABC và tam giác DEF có:
B
^
D
^
90
o
, ACFE,
A
^
E
^
. Tính độ dài AB biết DE 5cm A. 4 cm B. 3 cm C. 5 cm D. 6 cm
Đọc tiếp
Cho tam giác ABC và tam giác DEF có: B ^ = D ^ = 90 o , AC=FE, A ^ = E ^ . Tính độ dài AB biết DE = 5cm
A. 4 cm
B. 3 cm
C. 5 cm
D. 6 cm
Cho tam giác ABC, góc A<90o. Trên các cạnh AB,AC lần lượt lấy các điểm M,N ko trùng với các đỉnh của tam giác. BC>MN hay ko? Vì sao?
Xét \(\Delta AMN\) có : \(AM+AN>MN\)
Xét \(\Delta ABC\) có : \(AB+AC>BC\)
Mà \(\left\{{}\begin{matrix}AM< AB\\AN< AC\end{matrix}\right.\) \(\Leftrightarrow AB+AC>AM+AN\)
\(\Leftrightarrow BC>MN\)
Đúng 2
Bình luận (1)