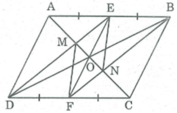
Cho hình bình hành ABCD. E và F theo thứ tự là trung điểm của AD; BC. Đường chéo AC cắt đoạn BE; DF tại P và Q.
a) CMR: AP=PQ=QC.
b) Lấy điểm M bất kỳ trên đoạn DC. Gọi I và K theo thứ tự là các điểm đối xứng của M qua E; F. CMR: I; K nằm trên đường thẳng AB.
c) CMR: Khi M di chuyển trên cạnh CD thì AI+AK không đổi.