Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình thoi ABCD có BD = 2a và AC = 8a. Tính a biết diện tích của hình thoi ABCD là 32cm2 .
Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)
\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)
\(\Rightarrow8a^2=32\)
\(\Rightarrow a^2=4\)
\(\Rightarrow a=2\left(cm\right)\)
Cho hình thoi ABCD có cạnh bằng 2a , ABC=60 độ . Tính độ dài của véc tơ AC .
Cho hình lăng trụ đứng ABCD. A’B’C’D’ có đáy là hình thoi, biết AA’ = 4a, AC = 2a, BD =a . Thể tích của khối lăng trụ là
A. 2 a 3
B. 8 a 3
C. 8 a 3 3
D. 4 a 3
Cho hình lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy là hình thoi, biết A A ' = 4 a , A C = 2 a , B D = a . Thể tích của khối lăng trụ là
A. 2 a 3
B. 8 a 3
C. 8 a 3 3
D. 4 a 3
Đáp án D
V = A A ' . S A B C D = A A ' . A C . B D 2 = 4 a 3 .
Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2a, A C = 3 a là tam giác đều, S A = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3
+ Tam giác SAB đều ⇒ S A = S B = A B = 2 a
+ Xét tam giác SAD có
S D 2 = S A 2 + A D 2 - 2 S A . S D . c o s S A D = 12 a 2 ⇒ S D = 2 3 a
+ Gọi A C ∩ B D = O ⇒ A O = A C 2 = 3 a 2
⇒ B O = A B 2 - A O 2 = 13 a 2 ⇒ B D = 13 a
Áp dụng công thức Hêrông ta tính được diện tích của tam giác SBD là S ∆ S B D = 183 a 2 4
+ Gọi H là hình chiếu của A trên (SBD). Vì A B = A D = A S = 2 a ⇒ H là tâm đường tròn ngoại tiếp tam giác
S B D ⇒ S H = S B . S D . B D 4 S ∆ S B D = 4 39 a 183
⇒ A H = S A 2 - S H 2 = 4 a 2 - 624 a 2 183 = 6 3 183 ⇒ v S . A B D = V A . S B D = 1 3 . A H . S ∆ S B D = 1 3 . 6 3 a 183 . 183 a 3 4 = 3 a 3 4 ⇒ V S . A B C D = 2 V S . A B C D = 3 a 3
Cách 2:
Ta có
c o s B A C = A B 2 + A C 2 - B C 2 2 . A B . A C = 4 a 2 + 3 a 2 - 4 a 2 2 . 2 a . 3 a = 3 4 ⇒ c o s B A D = 2 ( c o s B A C ) 2 - 1 = - 5 8
Áp dụng công thức tính nhanh cho khối chóp A.SBD ta có
V
A
.
S
B
D
=
A
S
.
A
B
.
A
D
2
.
Chọn đáp án A.
Cho hình chóp S.ABCD có đá ABCD là hình thoi cạnh 2 a , A C = 3 a , S A B là tam giác đều, S A D ^ = 120 ° . Tính thể tích khối chóp S.ABCD
A. 3 a 3
B. 3 3 a 3 2
C. 6 a 3
D. 2 3 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, A C = a 3 , SAB là tam giác đều, S A D ^ = 120 ° . Tính thể tích của khối chóp S.ABCD
A. a 3 3
B. 3 a 3 3 2
C. a 3 6
D. 2 a 3 3 3
HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD
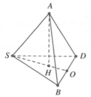
Bán kính đường tròn ngoại tiếp ∆SBD là
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, A D C ^ = 60 ∘ . Gọi O là giao điểm của AC và BD, SO vuông góc với (ABCD) và SO=a. Góc giữa đường thẳng SD và (ABCD) bằng
A. 60 ∘
B. 75 ∘
C. 30 ∘
D. 45 ∘
