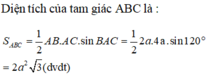Cho tam giác ABC có góc B=1200; BC=12cm; AB=6cm, đường phân giác BD. Kẻ AH vuông góc đường thẳng BC(H thuộc đường thẳng BC). Tính tỉ số lượng giác của góc HAB, từ đó suy ra tỉ số lượng giác của góc ABH
H24
Những câu hỏi liên quan
Cho tam giác ABC có AB 2a; AC 4a và góc BAC
120
0
. Tính diện tích tam giác ABC ? A.
S
8
a
2
. B.
S
2
a
2
3
C.
S
a
2
3
. D. ...
Đọc tiếp
Cho tam giác ABC có AB = 2a; AC = 4a và góc BAC = 120 0 . Tính diện tích tam giác ABC ?
A. S = 8 a 2 .
B. S = 2 a 2 3
C. S = a 2 3 .
D. S = 3 a 2 3
Cho tam giác ABC có , biết . Số đo của góc A là: A. 300 B. 600 C.900 D. 1200
Đọc tiếp
Cho tam giác ABC có 
, biết 
. Số đo của góc A là:
A. 300 B. 600 C.900 D. 1200
Cho tam giác ABC có a2 = b2 + c2 − bc. Góc B bằng bao nhiêu?
A. 1500 B. 1200 C. 600 D. 300
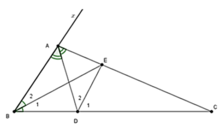
Cho tam giác ABC có A ^ = 120 0 . Các đường phân giác AD; BE. Tính số đo góc B E D ^
A. 55 0
B. 45 0
C. 60 0
D. 30 0
Cho tam giác ABC có góc A=1200. Có AD là tia phân giác của góc CAB.
Chứng minh 1/AD=1/AB+1/AC
Giải giúp mik với 🥺
Bài 3. Cho tam giác ABC có 
= 1200, các đường phân giác AD và BE. Tính số đo của góc BED.
Cho tam giác ABC vuông cân tại A, số đo góc B bằngA. 600 B. 900 C. 450 D. 1200
Đọc tiếp
Cho tam giác ABC vuông cân tại A, số đo góc B bằng
A. 600 | B. 900 | C. 450 | D. 1200 |
\(\widehat{A}=90^o\) \(\Rightarrow\widehat{B}+\widehat{C}=180^o-90^o=90^o\)
Do tam giác ABC la tam giac cân \(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{90^o}{2}=45^o\)
Chọn C
Đúng 4
Bình luận (0)
C
+)Do ΔABC là tam giác vuông cân tại A
=>\(\widehat{A}=90^o,\widehat{B}=\widehat{C}\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=90^o\)
\(=>\widehat{B}+\widehat{C}=180^o-\widehat{A}\)
\(=>\widehat{B}+\widehat{C}=180^o-90^o=90^o\)
Mà \(\widehat{B}=\widehat{C}=>\widehat{B}=\dfrac{90^o}{2}=45^o\)
Đúng 4
Bình luận (7)
Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có AB a,
B
A
C
^
120
0
. Biết thể tích khối chóp S.ABC bằng
3
a
3
4
góc giữa hai mặt phẳng (SBC) và (ABC) bằng A.
90...
Đọc tiếp
Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có AB = a, B A C ^ = 120 0 . Biết thể tích khối chóp S.ABC bằng 3 a 3 4 góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A. 90 0
B. 30 0
C. 60 0
D. 45 0
Phương pháp:
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng a ⊥ d trong mặt phẳng (Q) xác định đường thẳng b ⊥ d
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
Cách giải:
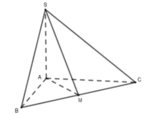
Gọi M là trung điểm BC => AM ⊥ BC (do ∆ ABC cân tại A).
Lại có ∆ SAB = ∆ SAC(c.g.c) hay ∆ SBC cân tại S
=> SM ⊥ BC
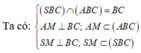
Theo đề bài
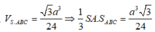
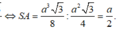
Lại thấy
∆
ABM vuông tại M có AB = a; 
Xét tam giác SAM vuông tại A có SA = AM = a 2 nên ∆ SAM vuông cân tại A hay ∠ S M A = 45 °
Vậy góc giữa (SBC) và (ABC) bằng 45 °
Chọn D.
Đúng 0
Bình luận (0)