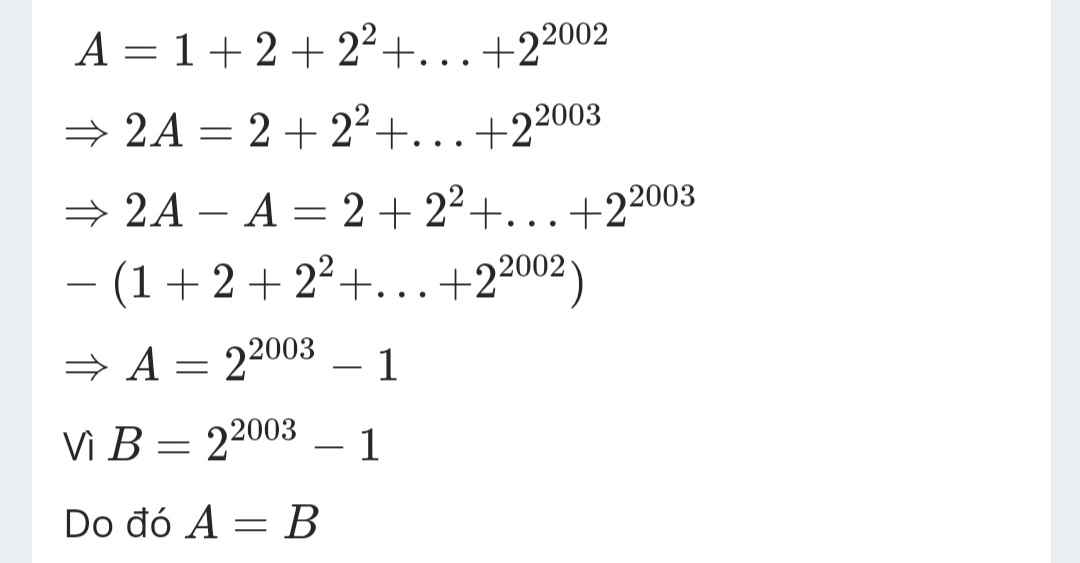So sánh A=2002^2; B=2001*2003
PA
Những câu hỏi liên quan
Cho A= 1+2002+20022+20023+......+200272
B=200273-1 so sánh A và B
So sánh A=2002^2,B=2001×2003
Có : A = 2002^2 = 2002.2002 = (2001+1).(2002 = 2001.2002+2002 = (2001.2002+2001)+1 = 2001.(2002+1)+1 = 2001.2003+1>2001.2003
=> A > B
k mk nha
Đúng 0
Bình luận (0)
Ta có :
\(B=2001x2003=2001x\left(2001+2\right)=2001^2+4002\)
\(A=2002^2=\left(2001+1\right)^2=2001^2+4002+1=2001^2+4003\)
=> A>B
Đúng 0
Bình luận (0)
Giải
A=2002^2
=2002x2002=2002(2001+1)=2002x2001+2002x1=2002x2001+2002
B=2001x2003
=2001x(2002+1)=2002x2001+2001x1=2002x2001+2001
Vì 2002>2001=>2002x2001+2002>2002x2001+2001=>A>B
Vậy.....
Đúng 0
Bình luận (0)
So Sánh :A=2001/2003 và B=2001+2002/2002+2003
So sánh 2 biểu thức A và B biết rằng:
A= 2000/2001 + 2001/2002
B= 2000 + 2001/ 2001+2002
Ta có:
\(\frac{2000}{2001}\)> \(\frac{2000}{2001+2002}\)(1)
\(\frac{2001}{2002}\)> \(\frac{2001}{2001+2002}\)(2)
Cộng các bất đẳng thức (1) và ( 2) vế với nhau:
Vậy \(\frac{2000}{2001}\)+ \(\frac{2001}{2002}\)> \(\frac{2000+2001}{2001+2002}\)hay A > B.
Đúng 0
Bình luận (0)
So sánh 2 biểu thức A và B, biết:
A = 2000/2001 + 2001/2002
B = 2000+2001/ 2001/2002
Trong phần câu hỏi tương tự có đó!
Đúng 0
Bình luận (0)
Cho A=2002/2001+2001/2002; B= 2000/2001+2001/2002 .So sánh A và B
Giải
Ta có\(A=\frac{2002}{2001}+\frac{2001}{2002}\)và \(B=\frac{2000}{2001}+\frac{2001}{2002}\)
Ta nhận xét thấy A và B cùng có chung 1 số hạng là \(\frac{2001}{2002}\)
Nên ta chỉ so sánh \(\frac{2002}{2001}\)và \(\frac{2000}{2001}\)ta so sánh 2 phân số đó với 1
Vì 2002>2001 nên \(\frac{2002}{2001}\)> 1
Vì 2000<2001 nên \(\frac{2000}{2001}\)<1
\(\Leftrightarrow\)\(\frac{2002}{2001}>\frac{2000}{2001}\)
\(\Leftrightarrow\)\(\frac{2002}{2001}+\frac{2001}{2002}>\frac{2000}{2001}+\frac{2001}{2002}\)
Vậy A>B
Đúng 0
Bình luận (0)
Cho A= 1 + 2 + 2^2 + … + 2^2002 và B = 2^2003 – 1. So sánh A và B
\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)
Đúng 0
Bình luận (0)
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+...+2^{2002}\right)\)
\(A=2^{2003}-1\)
⇒ \(A=B\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh 2 biểu thức A và B biết rằng :
A= 2000/2001+2001/2002
B=2000+2001/2001+2002
B=2000/2001+2002 + 2001/2001+2002
Ta có:
2000/2001 > 2000/2001+2002
2001/2002 > 2001/2001+2002
Vậy A >B
Đúng 0
Bình luận (0)
\(B=\frac{2000}{2001}+2002+\frac{2001}{2001}+2002\)
Ta có: \(\frac{2000}{2001}>\frac{2000}{2001}+2002\)
\(\frac{2001}{2002}>\frac{2001}{2001}+2002\)
Vậy A>B
Đúng 0
Bình luận (0)
Bạn Hoàng và sakura thủ..... bài y như copy xong rồi cải tiến ýkkkkkkkkkkkkk
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A= 2000/2001 + 2001/2002
B= 2000+2001/ 2001+2002
Không so sánh mà hãy so sánh A và B
kl của bạn sai nhưng mình vẫn tìm ra :
A>B
Đúng 0
Bình luận (0)
đề lạ zậy ko so sánh mà bảo so sánh!!!!!!! chả hỉu *_*!
765885
Đúng 0
Bình luận (0)