Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAˆ. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD.
A. 5 6
B. 7 6
C. 1 6
D. 3 4
Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAˆ. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD
A. 5 6
B. 7 6
C. 1 6
D. 3 4
Do M là trung điểm của BC nên:
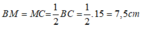
Theo tính chất tia phân giác của góc ta có:
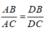
Suy ra:
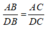
Theo tính chất của dãy tỉ số bằng nhau ta có:
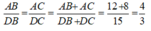
Suy ra:
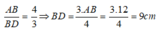
Do đó:
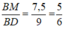
Chọn đáp án A
CHo tam giác ABC có AB=25cm, BC= 20 cm, CA= 24 cm, đường phân giác trong AD, đường phân giác AE. GỌi AM là đường trung tuyến của tam giác ADE. TAm giác ADE là tam giác gì?Tính DE và AM.
Cho TAm giác ABC có AM là đường Trung tuyến(M thuộc BC). Tia phân giác của Góc AMB cắt AB tại D. Tia phân giác của Góc AMC cắt AC tại E
a)Tính AD/BD biết AM=6,BC=10
b)CM BM/AM=CE/AE
c) CM : DE song song với BC
a) \(BM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
Tam giác ABM có MD là p/giác
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{AM}{BM}=\dfrac{6}{5}\)
b) Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{MC}{AM}=\dfrac{EC}{AE}\)
Mà: MC = BM (GT)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{EC}{AE}\)
c) Có: \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\left(cmt\right)\) (1)
Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{MC}\)
Mà: BM = MC (GT)
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{BM}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\)
=> DE // BC
a) Ta có: M là trung điểm của BC(gt)
nên \(MB=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔAMB có MD là đường phân giác ứng với cạnh AB(Gt)
nên \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{BD}=\dfrac{6}{5}\)
Cho tam giác ABC có AB bằng 4 cm AC bằng 12 cm BC = 6 cm các đường phân giác trong AD be cắt AB tại I
a, Tính BD và CD
b, Gọi AM là đường trung tuyến và G là trọng tâm tam giác ABC . C/m IG//BC và tính độ dài IG
Bài 1: Cho tam giác ABC vuông tại A có đường phân giác BD, đường trung tuyến AM, đường cao AH.
a) Tính AB, BC, AH, AM. Biết AD = 3 cm; CD = 5 cm.
b) Gọi I, K lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng AM vuông góc vs IK.
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(Gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{AB}{3}=\dfrac{BC}{5}\)
Ta có: AD+CD=AC(D nằm giữa A và C)
nên AC=3+5=8(cm)
Đặt \(\dfrac{AB}{3}=\dfrac{BC}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=3k\\BC=5k\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\left(3k\right)^2+8^2=\left(5k\right)^2\)
\(\Leftrightarrow9k^2+64=25k^2\)
\(\Leftrightarrow16k^2=64\)
\(\Leftrightarrow k^2=4\)
hay k=2
Suy ra: \(\left\{{}\begin{matrix}AB=3\cdot k=3\cdot2=6\left(cm\right)\\BC=5\cdot k=5\cdot2=10\left(cm\right)\end{matrix}\right.\)
Vậy: AB=6cm; BC=10cm
Cho tam giác ABC có cạnh BC= 9.95 cm, góc ABC= 114°43'12", góc BCA= 20°46'48". Từ A vẽ các đường cao AH, đường phân giác trong AD, đường phân giác ngoài AE, và đường trung tuyến AM. Tính độ dài các cạnh còn lại của tam giác ABC và các đoạn thẳng AH, AD, AE, AM ( làm tròn kết quả đến hàng phần trăm )
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM và đường phân giác
trong AD. Biết AB=21 cm BC = 35cm
| a) Giải tam giác ABC. | b) Tính độ dài AH, HC, AM, AD |
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=35^2-21^2=784\)
hay AC=28cm
Xét ΔBAC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{ABC}\simeq53^0\)
\(\Leftrightarrow\widehat{ACB}=37^0\)
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.
a) Cm: tam giác BDK vuông cân tại D
b) Cm : (AD/AC)2 = 2/9
2/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.
a) Cm: BI vuông với IM tại I
b) Cm: AN.AB = IC.MK
Cho tam giác ABC có đường trung tuyến AM. Đường phân giác của góc AMB cắt
cạnh AB ở E, đường phân giác của góc AMC cắt AC ở F.
a) Chứng minh:
EA/EB = FA/FB
, từ đó chứng minh rằng EF // BC
b) Gọi I là giao điểm của EF và AM. Chứng minh I là trung điểm của EF
c) Biết AM = 7 cm, BC = 12 cm. Tính tỉ số diện tích hai tam giác AMF và MFC
d) Kẻ tia FM cắt tia AB tại K. Chứng minh rằng: KB.EA=KA.EB