Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
A. R = 25
B. R = 25/2
C. R = 15
D. R = 20
Cho tam giác ABC vuông tại A có AB = 12cm, BC = 15cm. Diện tích tam giác ABC là :
\(S=\dfrac{12\cdot9}{2}=6\cdot9=54\left(cm^2\right)\)
bổ sung
A. 108cm2 B. 54cm C. 54cm2 D. 15cm2
Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)
=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)
=> \(DF=\sqrt{144}=12\left(cm\right)\)
Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh
Xét tam giác ABC và tam giác DEF ta có :
\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)
\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)
\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)
=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)
=> Tam giác ABC đồng dạng tam giác DEF
Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được
hai tam giác ko thể đồng dạng bạn nhé
a) Cho tam giác ABC vuông tại A có BC=15cm, AB:AC=3:4. Tính độ dài cạnh AB, AC
b) Cho tam giác ABC vuông tại A có AB=24cm, AC:BC=5:13. Tính độ dài cạnh AC,BC
Mình làm mẫu cho bạn câu a) nhé
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé
Cho tam giác ABC vuông tại A có BC = 15cm, AB = 12cm. Tính AC, B ^
A. AC = 8 (cm); B ^ ≈ 36 0 52 '
B. AC = 9 (cm); B ^ ≈ 36 0 52 '
C. AC = 9 (cm); B ^ ≈ 37 0 52 '
D. AC = 9 (cm); B ^ ≈ 36 0 55 '
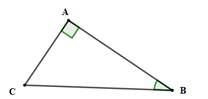
Xét tam giác ABC vuông tại A có:
Đáp án cần chọn là: B
cho tam giác ABC vuông tại A có AB/AC=0,75 và BC=15cm .khi đó chu vi của tam giác ABC là...
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm và tam giác MNP vuông tại M có MN=9cm, NP=15cm.
a) tính cạnh BC và MP
b) tam giác ABC có đồng dạng tam giác MNP không? Vì sao?
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
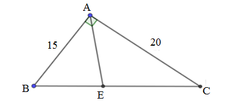
Giải tam giác ABC:
A. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
B. BC = 25; B ^ = 53 0 8 ' ; C ^ = 53 0 8 '
C. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
D. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
Áp dụng định lý Pytago cho vuông tại A có:
![]()
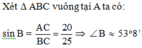

Đáp án cần chọn là: B
a, Cho tam giác ABC vuông tại A có AB =3/5 BC . Đường cao AH =12cm . Tính chu vi tam giác ABC .
b, Cho tam giác ABC vuông tại A có đường cao AH , phân giác AD . Biết BD=15cm ,DC=20cm.Tính AH,AD
GIÚP MIK . THANKS
a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm
Giúp mình với ak!!!!
1. Cho tam giác ABC vuông tại A, biết AB/AC=5/7 và đường cao AH=15cm. Tính HB, HC.
2. Cho tam giác ABC vuông tại A, có đường cao AH=14cm và HB/HC=1/4. Tính chu vi tam giác ABC.
1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)