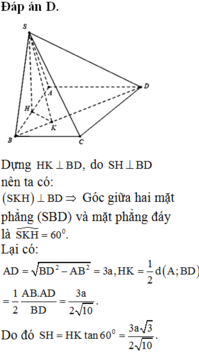
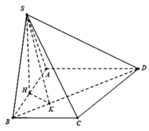
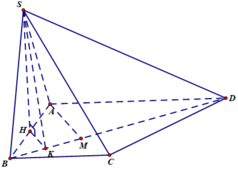
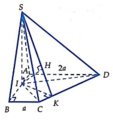
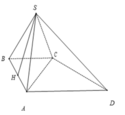
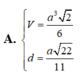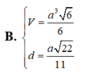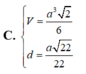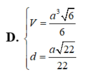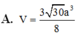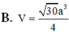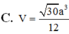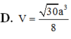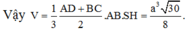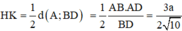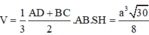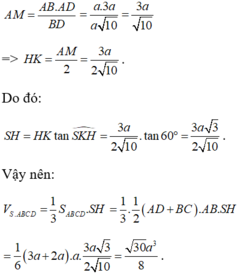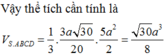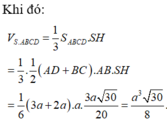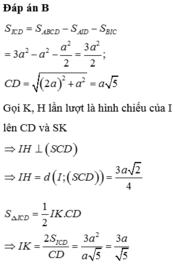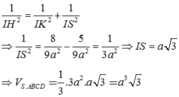Cho hình chóp S.ABCD đáy ABCD là hình thang vuông tại A và B, I là trung điểm của AB, có (SIC) và (SID) cùng vuông góc với đáy. Biết ADAB2a, BCa, khoảng cách từ I đến (SCD) là
3
a
2
4
.
Khi đó thể tích khối chóp S.ABCD là A.
a
3
.
B.
a
3
3
.
C. ...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình thang vuông tại A và B, I là trung điểm của AB, có (SIC) và (SID) cùng vuông góc với đáy. Biết AD=AB=2a, BC=a, khoảng cách từ I đến (SCD) là
3
a
2
4
.
Khi đó thể tích khối chóp S.ABCD là
A.
a
3
.
B.
a
3
3
.
C.
3
a
3
.
D.
a
3
3
2
.