Đáp án B
S I C D = S A B C D − S A I D − S B I C = 3 a 2 − a 2 − a 2 2 = 3 a 2 2 ; C D = 2 a 2 + a 2 = a 5
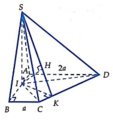
Gọi K, H lần lượt là hình chiếu của I lên CD và SK
⇒ I H ⊥ S C D ⇒ I H = d I ; S C D = 3 a 2 4
S Δ I C D = 1 2 I K . C D ⇒ I K = 2 S I C D C D = 3 a 2 a 5 = 3 a 5
1 I H 2 = 1 I K 2 + 1 I S 2 ⇒ 1 I S 2 = 8 9 a 2 − 5 9 a 2 = 1 3 a 2 ⇒ I S = a 3
⇒ V S . A B C D = 1 3 .3 a 2 . a 3 = a 3 3

