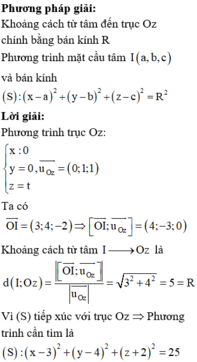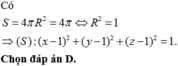Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau: Có tâm I(5; -3; 7) và có bán kính r = 2.
PB
Những câu hỏi liên quan
Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau: Có tâm là điểm C(4; -4; 2) và đi qua gốc tọa độ
Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau: Đi qua điểm M(2; -1; -3) và có tâm C(3; -2; 1)
Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau :
a) Có tâm \(I\left(5;-3;7\right)\) và có bán kính \(r=2\)
b) Có tâm là điểm \(C\left(4;-4;2\right)\) và đi qua gốc tọa độ
c) Đi qua điểm \(M\left(2;-1;-3\right)\) và có tâm \(C\left(3;-2;1\right)\)
a) \(\left(x-5\right)^2+\left(y+3\right)^2+\left(z-7\right)^2=4\)
b) \(\left(x-4\right)^2+\left(y+4\right)^2+\left(z-2\right)^2=36\)
c) \(\left(x-3\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=18\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và tiếp xúc với đường thẳng A.
(
x
-
1
)
2
+
y
2
+
(
z...
Đọc tiếp
Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và tiếp xúc với đường thẳng
![]()
A. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 81
B. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 9
C. ( x + 1 ) 2 + y 2 + ( z - 1 ) 2 = 81
D. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 3
Đáp án B
Đường thẳng d đi qua điểm M(6 ;1 ;0) và có vectơ chỉ phương là u d → = (4; -1; -1). Ta có:
![]()
Do đường thẳng d tiếp xúc với mặt cầu (S) nên (S) có bán kính là:
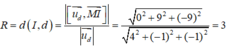
Vậy phương trình của mặt cầu (S) là : ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 9
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm
I
(
3
;
4
;
−
2
)
.
Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz. A.
S
:
x
−
3
2
+
y
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm I ( 3 ; 4 ; − 2 ) . Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
A. S : x − 3 2 + y − 4 2 + z + 2 2 = 25
B. S : x − 3 2 + y − 4 2 + z + 2 2 = 4
C. S : x + 3 2 + y + 4 2 + z − 2 2 = 20
D. S : x − 3 2 + y − 4 2 + z + 2 2 = 5
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz. A.
(
S
)
:
x
-
3
2
+
y
-
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
A. ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 25
B. ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 4
C. ( S ) : x + 3 2 + y + 4 2 + z - 2 2 = 20
D. ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 5
Đáp án A
Phương pháp giải:
Khoảng cách từ tâm đến trục Oz chính bằng bán kính R
Phương trình mặt cầu tâm và bán kính
![]()
Lời giải:
Phương trình trục Oz
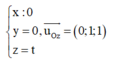
Ta có
![]()
Khoảng cách từ tâm I -> Oz là
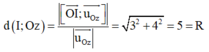
Vì (S) tiếp xúc với trục Oz Þ Phương trình cần tìm là ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 25
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình
x
+
1
2
+
y
+
3
2
+
z
2
5.
Tọa độ tâm I và bán kính mặt cầu là A.
I
1
;
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x + 1 2 + y + 3 2 + z 2 = 5. Tọa độ tâm I và bán kính mặt cầu là
A. I 1 ; − 3 ; 0 , R = 5
B. I 1 ; 3 ; 0 , R = 5
C. I − 1 ; 3 ; 0 , R = 5
D. I 1 ; − 3 ; 0 , R = 5
Đáp án A
Xét mặt cầu S : x − 1 2 + y + 3 2 + z 2 = 5 có tâm I 1 ; − 3 ; 0 và bán kính R = 5
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và cắt đường thẳng theo một dây cung AB có độ dài bằng 8 A.
(
x
-
1
)
2
+
y
2
+
...
Đọc tiếp
Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và cắt đường thẳng ![]() theo một dây cung AB có độ dài bằng 8
theo một dây cung AB có độ dài bằng 8
A. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 16
B. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 5
C. ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 25
D. (x + 1)2 + y2 + (z - 1)2 = 25
Đáp án C
Đường thẳng d đi qua điểm M(-2 ;3 ;2) và có vectơ chỉ phương là u d → = (-4; 1; 1). Ta có:

Đúng 0
Bình luận (0)
Trong không gian Oxyz, mặt cầu có tâm I(1;1;1) và diện tích bằng 4π có phương trình là A.
x
-
1
2
+
y
-
1
2
+
z
-
1
2...
Đọc tiếp
Trong không gian Oxyz, mặt cầu có tâm I(1;1;1) và diện tích bằng 4π có phương trình là
A. x - 1 2 + y - 1 2 + z - 1 2 = 4
B. x + 1 2 + y + 1 2 + z + 1 2 = 1
C. x + 1 2 + y + 1 2 + z + 1 2 = 4
D. x - 1 2 + y - 1 2 + z - 1 2 = 1