Cho đoạn thẳng AB=5cm Gọi M là trung điểm.Vẽ đường tròn (I; 2,5cm). trên IB vẽ sao cho IK=bốn cm. tính KB
TK
Những câu hỏi liên quan
Cho đoạn thẳng AB dài 5cm. vẽ đường tròn tâm A, bán kính 2cm. Gọi M là giao điểm của đường tròn (A;2cm) và AB. Tính MB
cho đoạn thẳng AB =5cm , I là trung điểm của AB .Vẽ đường tròn tâm A bán kính là 3cm và đường tròn tâm B , bán kính là BI . 2 đường tròn cắt nhau tại 2 điểm C,D . Tính độ dài đoạn thẳng AD và BC?
Vì 2 đường tròn tâm A bán kính 3cm và đường tròn tâm B bán kính BI cắt nhau tại điểm D nên đoạn thẳng AD=3cm
Vì I là trung điểm của đoạn thẳng AB nên BI=AB/2=5/2=2.5(cm)
Vì 2 đường tròn tâm A bán kính 3cm và đường tròn tâm B bán kính 2,5cm cắt nhau tại điểm C nên đoạn thẳng BC=2,5cm
Vậy đoạn thẳng AD=3cm; BC=2,5cm
Mình cũng k chắc là làm đúng
Chúc bạn học tốt!^_^
Đúng 0
Bình luận (0)
Bài 7: Vẽ đoạn thẳng AB = 5cm. Lấy điểm M sao cho A, B, M không thẳng hàng.Vẽ đường thẳng AM, đoạn thẳng AB. Gọi O là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng OA
giúp mik vs :(
vvẽ đoạn thẳng AB dài 3 cm.vẽ đường tròn(A;2 cm) và đường tròn (B: 2 cm).gọi giao điểm của 2 đường tròn là C;D.vẽ đoạn thẳng C;D.gọi giao điểm của AB và CD là I. đo độ dài đoạn thẳng IA và IB và cho biết I có là trung điểm đoạn thẳng AB ko
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C ≠A . Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC
b) Chứng minh A, I, C, M cùng nằm trên 1 đường tròn
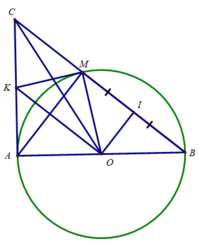
b) Tam giác ACO vuông tại A ⇒ Tâm đường tròn ngoại tiếp tam giác ACO là trung điểm của CO (1)
Xét tam giác AMB có:
I là trung điểm của AM
O là trung điểm của AB
⇒ IO là đường trung bình của tam giác AMB
⇒ IO // AM
Mà AM ⊥ MB ⇒ IO ⊥ MB
Tam giác CIO vuông tại I ⇒ Tâm đường tròn ngoại tiếp tam giác CIO là trung điểm của CO (2)
Từ (1) và (2) ⇒ 4 điểm A, I, C, O cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
Vẽ đoạn thẳng ab = 5cm vẽ đường tròn. vẽ đường tròn (A,4cm) và (B;2cm),chúng cắt nhau tại C và D.
a)tính độ dài đoạn thẳng AC và BC
b)gọi K là trung điểm của đoạn thẳng AB . chứng tỏ điểm K nằm bên trong đường tròn (A,4cm)
Cho nửa đường tròn đường kính $AB$. Trên đoạn $AB$ lấy điểm $M$, gọi $H$ là trung điểm $AM$. Đường thẳng qua $H$ vuông góc với $AB$ cắt nửa đường tròn đã cho tại $C$. Đường tròn đường kính $MB$ cắt $CB$ tại $I$. Chứng minh $HI$ là tiếp tuyến của đường tròn đường kính $MB$.
Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên ^MIB=90o⇒^CIM=90o.
Vậy nên tứ giác CHMI nội tiếp.
⇒^HIM=^HCM.
Tam giác ACM cân tại C nên ^HCM=^HCA.
Mà ^HCA=^HBC (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên ^HBC=^JIB.
Tóm lại : ^HIM=^JIB⇒^HIM+^MIJ=^JIB+^MIJ
⇒^HIJ=^MIB=90o.
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB
Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên .
Vậy nên tứ giác CHMI nội tiếp.
.
Tam giác ACM cân tại C nên .
Mà (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên .
suy ra :
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB.
gọi O là trung điểm của AB
E là trung điểm của MB
có tam giác IMB là tam giác nội tiếp đường tròn tâm E
⇒tam giác IMB vuông tại I
⇒góc MIB bằng 90độ
⇒góc CIM bằng 90 độ
⇒tứ giác CHMI là nội tiếp
⇒góc HIM bằng góc HCM
có H là trung điểm của AM
CH là trung tuyến của tam giác CAM
có CH vuông góc với AM
⇒CH là đường cao
xét tam giác CAM có
CH là đường cao(cmt)
CH là trung tuyến(cmt)
⇒tam giác CAM cân tại C
⇒góc HCM bằng góc HCA
mà góc HCA bằng góc HBC (cùng phụ góc ACB)
có E là trung điểm của MB(lấy thêm)⇒IE là trung tuyến
xét tam giác MIB vuông tại I có
IE là trung tuyến
⇒IE bằng 1/2MB
mà ME bằng MB bằng 1/2MB
⇒IE bằng ME(1/2MB)
xét tam giác EIB có IE bằng ME (cmt)
⇒tam giác EIB cần tại E
⇒góc EBI bằng góc EIB
mà góc HCA bằng góc HBC
⇒góc EIB bằng góc HCA
có góc HIM bằng góc EIB
⇒góc HIM+gócMIE bằng góc EIB+góc MIE
⇒góc HIE bằng góc MIB bằng 90 độ
⇒ HI là tiếp tuyến tại I của đường trong đường kính MB
Xem thêm câu trả lời
Cho đoạn thẳng AB 6 cm, lấy M là trung điểm của đoạn thẳng AB. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tròn tâm B bán kính 5 cm cắt nhau tại C và D.a) Xác định vị trí các điểm A, D, M đối với đường tròn (B; 5cm)b) Tính chu vi của tứ giác ACBD.
Đọc tiếp
Cho đoạn thẳng AB = 6 cm, lấy M là trung điểm của đoạn thẳng AB. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tròn tâm B bán kính 5 cm cắt nhau tại C và D.
a) Xác định vị trí các điểm A, D, M đối với đường tròn (B; 5cm)
b) Tính chu vi của tứ giác ACBD.
a) A nằm ngoài đường tròn ( B; 5cm) vì BA = 6cm > 5cm.
M nằm trong đường tròn ( B; 5cm) vì BM == 3cm < 5cm.
D nằm trên đường tròn ( B; 5cm)vì BD = 5cm
b) Chu vi của tứ giác ACBD = AC + BC + BD + AD = 14cm.
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB 6 cm, lấy M là trung điểm của đoạn thẳng AB. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tròn tâm B bán kính 5 cm cắt nhau tại C và D.a) Xác định vị trí các điểm A, D, M đối với đường tròn (B; 5cm)b) Tính chu vi của tứ giác ACBD.
Đọc tiếp
Cho đoạn thẳng AB = 6 cm, lấy M là trung điểm của đoạn thẳng AB. Vẽ đường tròn tâm A bán kính 2cm và đường tròn tròn tâm B bán kính 5 cm cắt nhau tại C và D.
a) Xác định vị trí các điểm A, D, M đối với đường tròn (B; 5cm)
b) Tính chu vi của tứ giác ACBD.
a) A nằm ngoài đường tròn ( B; 5cm) vì BA = 6cm > 5cm.
M nằm trong đường tròn ( B; 5cm) vì BM =3cm < 5cm.
D nằm trên đường tròn ( B; 5cm)vì BD = 5cm
b) Chu vi của tứ giác ACBD = AC + BC + BD + AD = 14cm.
Đúng 0
Bình luận (0)