Phương trình đường tròn có tâm I(3; -5) và có bán kính R = 2 là
A. x 2 + y 2 + 3 x − 5 y + 2 = 0
B. x 2 + y 2 + 6 x − 10 y + 30 = 0
C. x 2 + y 2 - 6 x + 10 y - 4 = 0
D. x 2 + y 2 − 6 x + 10 y + 30 = 0
1. viết phương trình đường tròn ngoại tiếp tam giác ABC biết A(-1,1);B(1,3);C(1,-1)
2. viết phương trình đường tròn có tâm I(-2,3) và đi qua M(2,-3)
3. viết phương trình đường tròn có tâm I nằm trên đường thẳng 4x-2y-8=0 biết đường tròn đó tiếp xúc với trục tọa độ
Lập phương trình đường tròn trong mỗi trường hợp sau:
a) Đường tròn có tâm I(- 3 ; 4) bán kính R = 9;
b) Đường tròn có tâm I(5 ;-2) và đi qua điểm M(4;- 1);
c) Đường tròn có tâm I(1;- 1) và có một tiếp tuyến là A: 5x- 12y – 1 = 0;
d) Đường tròn đường kính AB với A(3;-4) và B(-1; 6);
e) Đường tròn đi qua ba điểm A(1;1), B(3; 1), C(0; 4).
a) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)
b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}} = \sqrt 2 \)
Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)
c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)
d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)
Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}} = \sqrt {29} \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)
e) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\) b
Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)
Bài 1: a) Viết phương trình đường tròn có tâm \(I(3;-1)\) và cắt \(d:2x-5y+18=0\) theo một dây cung có độ dài bằng 6
b) Viết phương trình đường tròn có tâm \(I(-1;2)\) và cắt đường thẳng \(d: x-5y-2=0\) theo một dây cung có độ dài bằng \(\sqrt{26}\)
Bài 2: Trong mặt phẳng \(Oxy\), cho đường tròn \((C): x^2+y^2+2x-4y-20=0\) và điểm \(A(3;0)\). Viết phương trình đường thẳng \(\Delta\) đi qua \(A\) và cắt đường tròn \((C)\) theo một dây cung MN sao cho
a) MN có độ dài lớn nhất b) MN có độ dài nhỏ nhất
gọi M,N là hai điểm cắt đg tròn tâm I
kẻ IH vuông góc với MN ,theo đề bài ta có MN =6 => MH=3
độ dài từ tâm I đến (d) =\(\dfrac{\left|2.3-5.-1+18\right|}{\sqrt{2^2+\left(-5\right)^2}}=\sqrt{29}\)
Áp dụng pytago vào tam giác vuông IMH ta có
\(IM=\sqrt{IH^2+MH^2}=\sqrt{38}\)
vậy pt đg tròn là \(\left(x-3\right)^2+\left(y+1\right)^2=\left(\sqrt{38}\right)^2\)( tới đây bạn tự khai triển ra nha
b ) cách làm tương tự
2 .
MN max khi nó là đường kính > nó phải đi qua điểm I
\(\overrightarrow{uIA}=\left(4;-2\right)=>n\overrightarrow{IA}=\left(2;4\right)\)
ptđt \(\Delta:2\left(x-3\right)+4\left(y-0\right)=0\)
MN min
ta có MN=2HM
trg tam giác vuông IHMtheo pytago ta có \(HM=\sqrt{IA^2-IH^2}\)có IA là bán kính ( cố định ) => IH max thì MN min
lại xét tam giác IHP trong tam giác IHP thì có IP là cạch huyền mà trg tam giác cạc huyền là cạch lớn nhất nên IH max khi điểm H trùng với điểm P .
Đường tròn có tâm I(1; 2), bán kính R = 3 có phương trình là:
A. x 2 + y 2 + 2 x + 4 y − 4 = 0.
B. x 2 + y 2 + 2 x − 4 y − 4 = 0.
C. x 2 + y 2 − 2 x + 4 y − 4 = 0.
D. x 2 + y 2 − 2 x − 4 y − 4 = 0.
C : I 1 ; 2 R = 3 → C : x − 1 2 + y − 2 2 = 9 ⇔ x 2 + y 2 − 2 x − 4 y − 4 = 0.
Đáp án A
Cho đường tròn (C) có phương trình x 2 + y 2 + 4 x − 6 y − 3 = 0 . Khi đó đường tròn có tâm I và bán kính R với
A. I(4; -6), R = 4
B. I(-2; 3), R = 16
C.I(-4; 6), R = 4
D. I(-2; 3) , R = 4
Ta có x 2 + y 2 + 4 x − 6 y − 3 = 0 ⇔ x + 2 2 + y − 3 2 = 16 nên đường tròn có tâm I(-2; 3) và bán kính R = 4.
Chú ý. Học sinh có thể áp dụng công thức tính tâm và bán kính của đường tròn khi biết phương trình tổng quát của đường tròn
ĐÁP ÁN D
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.
a. Viết phương trình của đường tròn đó.
b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v=(-2 ;1).
c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.
d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
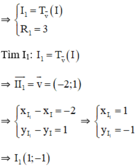
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒ 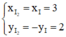 ⇒ I2(3; 2)
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒ 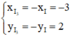
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
Đường tròn tâm I( 3; -1) và bán kính R= 2 có phương trình là
A.( x+ 3) 2+ (y+2) 2= 2
B.(x-3)2+ (y+ 2)2= 4
C. ( x+ 3) 2+(y-2) 2=4
D.(x-3)2+ (y-2) 2= 4
Phương trình đường tròn có tâm (3; -2) , bán kính R= 2 là:
(x-3)2+ (y+ 2)2= 4
Chọn B.
Đường tròn (C) tâm I( -4; 3) và tiếp xúc với trục tung có phương trình là
A. x2+ y2 - 4x + 3y + 1 = 0.
B. (x+ 4) 2+ (y- 3) 2= 16.
C.(x-4) 2+ (y+ 3) 2= 9.
D. x2+ y2 + 8x -6 y + 1 = 0.
Do đường tròn (C) tiếp xúc với trục tung Oy và có tâm I( -4; 3) nên:
a= - 4; b= 3 và R= |a| =4.
Do đó, (C) có phương trình: (x+ 4) 2+ (y- 3) 2= 16.
Chọn B.
Đường tròn (C) có tâm I( -1; 3) và tiếp xúc với đường thẳng d: 3x-4y + 5= 0 có phương trình là
A. (x+ 1) 2+ (y- 3) 2= 4.
B. (x+ 1) 2+ (y- 3) 2= 10
C. (x+ 1) 2+ (y- 3) 2= 8.
D. (x+ 1) 2+ (y- 3) 2= 16
Đường tròn có bán kính .
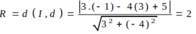
Vậy phương đường tròn là: (x+ 1) 2+ (y- 3) 2= 4.
Chọn A.