Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho A D = 3 A N . Tính thể tích của tứ diện B.MNP.
A. V 4
B. V 12
C. V 8
D. V 64
Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho A D = 3 A N . Tính thể tích của tứ diện BMNP.
A . V 4 .
B . V 12 .
C . V 8 .
D . V 64 .
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
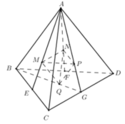
A. V 9
B. V 3
C. 2 V 9
D. V 27
Ta có:
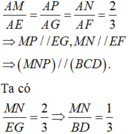
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
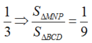
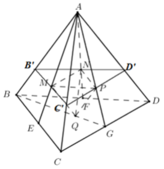
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
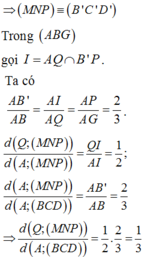

Chọn D.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Đáp án A
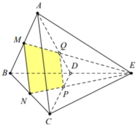
Nối ![]() chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích 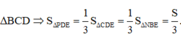
Họi h là chiều cao của tứ diện ABCD 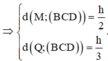
Khi đó 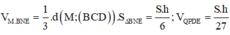
Suy ra
![]()
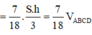

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
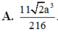
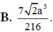
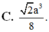
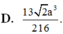
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
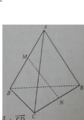
A. GM = GN
B. G M → + G N → = 0 →
C. G A → + G B → + G C → + G D → = 0
D. P G → = 1 / 4 ( P A → + P B → + P C → + P D → ) , với P là điểm bất kì.
Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
A. 7 2 a 3 216
B. 11 2 a 3 216
C. 13 2 a 3 216
D. 2 a 3 18
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
A. G A → + G B → + G C → + G D → = 0 →
B. 4 P G → = P A → + P B → + P C → + P D → với P là điểm bất kỳ
C. G M = G N
D. G M → + G N → = 0 →
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
![]()
![]() với P là điểm bất kỳ
với P là điểm bất kỳ
![]()
![]()