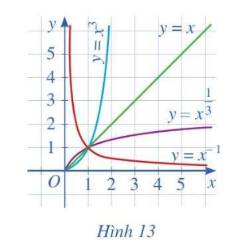
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
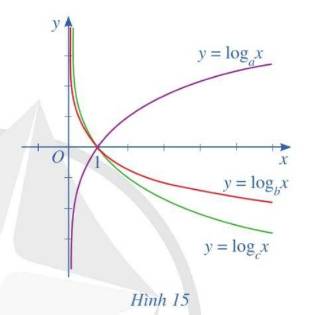
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.Hình vẽ bên là đồ thị của ba hàm số
y = x a , y = log b x , y = log c x , x > 0 .

Khẳng định nào sau đây đúng?
A. a < c < b
B. a > c > b
C. a > b > c
D. a < b < c
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.
Hình vẽ bên là đồ thị của ba hàm số y = x a , y = log b x , y = log c x , x > 0 .
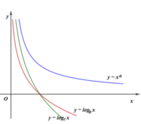
Khẳng định nào sau đây đúng?
A. a < c < b
B. a > c > b
C. a > b > c
D. a < b < c
Cho a là số thực tùy ý và b, c là các số thực dương khác 1.
Hình vẽ bên là đồ thị của ba hàm số y = x a , y = log b x , y = log c x , x > 0
Khẳng định nào sau đây đúng
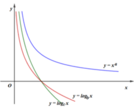
A. a<c<b
B. a<c<b
C. a>b>c
D. a<b<c
Nhận xét:
+) Đồ thị hàm số y = x a nghịch biến trên khoảng ( 0 ; + ∞ ) ⇒ a < 0
+) Xét đồ thị hàm số y = log b x v à y = log c x , x > 0
Cho y=1 ta có: log b x 1 = log c x 2 ⇔ x 1 = b , x 2 = c
Mà x 1 < x 2 ⇒ b < c ⇒ a < 0 < b < c . Vậy a<b<c
Chọn đáp án D.
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y = log a x , y = log b x và y = log c x được cho trong hình vẽ sau:
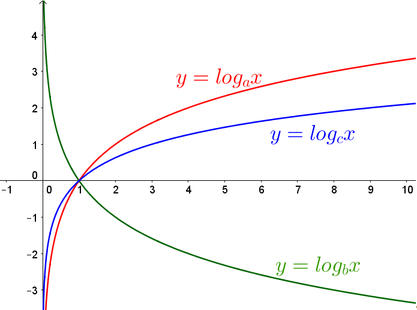
A. c < b < a
B. a < b < c
C. a < c < b
D. b < c < a
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y = log a x , y = log b x , y = log c x cho như hình vẽ
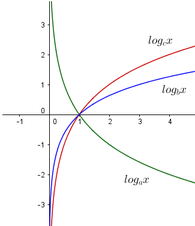
A. b > c > 1 > a
B. b > a > 1 > c
C. a > c > 1 > b
D. c > b > 1 > a
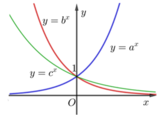
Trên hình 2.13, đồ thị của ba hàm số y = ax, y = bx, y = cx (a, b, c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c
![]()
![]()
![]()
![]()
Đáp án C
Dựa vào hình vẽ, ta thấy rằng:
Hàm số y = ax là hàm số đồng biến; hàm số y = bx, y = cx là hàm số nghịch biến.
Suy ra a > 1 và 0 < b < 1 0 < c < 1 → a > b ; c
Gọi B(-1; yB) thuộc đồ thị hàm số y = b x ⇒ y B = 1 b
Và C(-1;yc) thuộc đồ thị hàm số y = c x ⇒ y C = 1 c
Dựa vào đồ thị, ta có y B > y c ⇒ 1 b > 1 c ⇒ c > b
Trên hình 2.13, đồ thị của ba hàm số y = a x , y = b x , y = c x (a, b, c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c
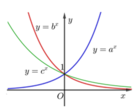
A. c > b > a
B. b > c > a
C. a > c > b
D. a > b > c
Đáp án C
Dựa vào hình vẽ, ta thấy rằng:
Hàm số y = a x là hàm số đồng biến; hàm số y = b x , y = c x là hàm số nghịch biến.
Suy ra a > 1 và 0 < b < 1 0 < c < 1 → a > b ; c .
Gọi B − 1 ; y B thuộc đồ thị hàm số y = b x ⇒ y B = 1 b ;
Và C − 1 ; y C thuộc đồ thị hàm số y = c x ⇒ y C = 1 c .
Dựa vào đồ thị, ta có y = c x ⇒ y C = 1 c .
Vậy hệ số a > c > b .
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y = log a x , y = log b x và y = log c x được cho trong hình vẽ sau:
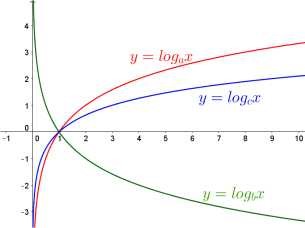
Mệnh đề nào sau đây đúng?
A. b < a < c
B. a < c < b
C. c < b < a
D. a < b < c