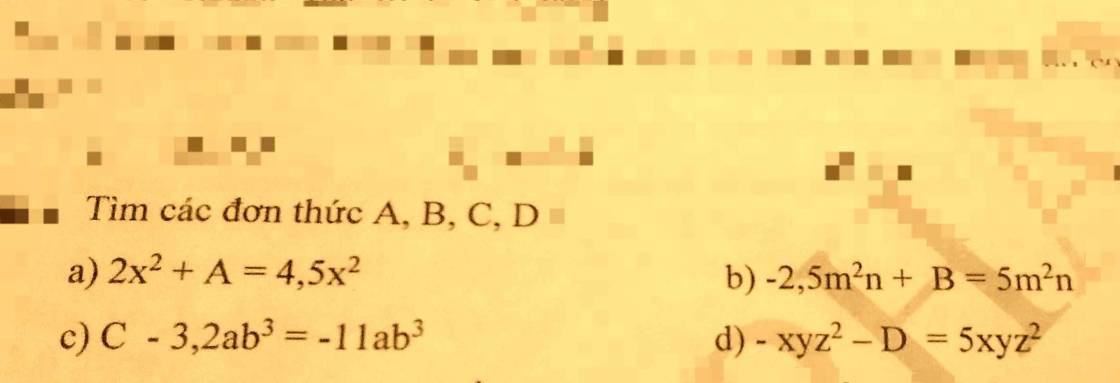Câu 1: Đa thức -2x^2y +xy + 1 đc viết thành tổng của 2 đa thức nào.
Câu 2 : Đa thức x^2y^2 + 2xy -3 đc viết thành tổng của 2 đa thức nào.
Câu 3 : Đa thức -2x^2y + xy +1 đc viết thành hiệu của 2 đa thức nào.
Câu 4 : Đa thức x^2y^2 -2xy +3 đc viết thành hiệu của 2 đa thức nào.
Phép nhân và phép chia các đa thức
Câu 1: Đa thức -2x^2y +xy + 1 đc viết thành tổng của 2 đa thức nào. Câu 2 : Đa thức x^2y^2 + 2xy -3 đc viết thành tổng của 2 đa thức nào. Câu 3 : Đa thức -2x^2y + xy +1 đc viết thành hiệu của 2 đa thức nào.Câu 4 : Đa thức x^2y^2 -2xy +3 đc viết thành hiệu của 2 đa thức nào.
Đọc tiếp
Câu 1:
-2x²y + xy + 1 = -2x²y + (xy + 1)
Vậy -2x²y + xy + 1 được viết thành tổng của hai đa thức: -2x²y và xy + 1
Câu 2:
x²y² + 2xy - 3 = x²y² + (2xy - 3)
Vậy x²y² + 2xy - 3 được viết thành tổng của hai đa thức: x²y² và 2xy - 3
Câu 3:
-2x²y + xy + 1 = (xy + 1) - 2x²y
Vậy -2x²y + xy + 1 được viết thành hiệu của hai đa thức: xy + 1 và 2x²y
Câu 4:
x²y² - 2xy + 3 = (x²y² + 3) - 2xy
Vậy x²y² - 2xy + 3 được viết thành hiệu của hai đa thức: x²y² + 3 và 2xy
Đúng 3
Bình luận (1)
Tìm 3 số lẻ liên tiêp, biết tích 2 số sau lớn hơn tích của 2 số đầu là 212
Gọi ba số lẻ liên tiếp là 2k+1;2k+3;2k+5
Theo đề, ta có: (2k+3)(2k+5)-(2k+1)(2k+3)=212
=>(2k+3)(2k+5-2k-1)=212
=>2k+3=212/4=53
=>2k=50
=>k=25
Vậy: Ba số cần tìm là 51;53;55
Đúng 1
Bình luận (0)
Gọi k là số tự nhiên \(k\in N\)
Số lẻ thứ nhất là: \(2k+1\)
Số lẻ thứ hai là: \(2k+3\)
Số tự nhiên thứ ba là: \(2k+5\)
Tích của 2 số lẻ đầu tiên là: \(\left(2k+1\right)\left(2k+3\right)\)
Tích của hai số lẻ sau là: \(\left(2k+3\right)\left(2k+5\right)\)
Mà tích của hai số lẻ sau lớn hơn tích của hai số lẻ đầu 212 nên ta có:
\(\left(2k+3\right)\left(2k+5\right)-\left(2k+1\right)\left(2k+3\right)=212\)
\(\Leftrightarrow4k^2+10k+6k+15-\left(4k^2+6k+2k+3\right)=212\)
\(\Leftrightarrow4k^2+16k+15-4k^2-8k-3=212\)
\(\Leftrightarrow\left(4k^2-4k^2\right)+\left(16k-8k\right)+\left(15-3\right)=212\)
\(\Leftrightarrow8k+12=212\)
\(\Leftrightarrow8k=212-12\)
\(\Leftrightarrow8k=200\)
\(\Leftrightarrow k=\dfrac{200}{8}\)
\(\Leftrightarrow k=25\left(tm\right)\)
Số lẻ thứ nhất là: \(2\cdot25+1=51\)
Số lẻ thứ hai là: \(2\cdot25+3=53\)
Số lẻ thứ ba là: \(2\cdot25+5=55\)
Đúng 0
Bình luận (0)
 chi tiết
chi tiết
a) \(5x^3yy^2\)
\(=5x^3y^3\)
Có bậc là:
\(3+3=6\)
b) \(5mn^2\cdot\left(-3\right)n\)
\(=5\cdot\left(-3\right)\cdot m\cdot\left(n^2\cdot n\right)\)
\(=-15mn^3\)
Có bậc là:
\(1+3=4\)
c) \(\dfrac{3}{4}\left(a^2b\right)^3\cdot2,5a^3\)
\(=\dfrac{3}{4}a^6b^3\cdot2,5a^3\)
\(=\dfrac{3}{4}\cdot2,5\cdot\left(a^6\cdot a^3\right)\cdot b^3\)
\(=\dfrac{15}{8}a^9b^3\)
Có bậc là:
\(9+3=12\)
d) \(1,5\left(pq\right)^2\cdot4p^3\cdot q^2\)
\(=1,5p^2q^2\cdot4p^3\cdot q^2\)
\(=1,5\cdot4\cdot\left(p^2\cdot p^3\right)\cdot\left(q^2\cdot q^2\right)\)
\(=6p^5q^4\)
Có bậc là:
\(5+4=9\)
Đúng 2
Bình luận (0)
a: \(5x^3y\cdot y^2=5x^3y^3\)
Bậc là 3+3=6
b: \(5mn^2\left(-3\right)n=-15mn^3\)
Bậc là 1+3=4
c: \(\dfrac{3}{4}\left(a^2b\right)^3\cdot2.5a^3=\dfrac{3}{4}\cdot\dfrac{5}{2}\cdot a^6b^3\cdot a^3\)
\(=\dfrac{15}{8}a^9b^3\)
Bậc là 9+3=12
d: \(1.5\left(p\cdot q\right)^2\cdot4p^3q^2\)
\(=1.5\cdot4\cdot p^2q^2\cdot p^3q^2=6p^5q^4\)
bậc là 5+4=9
Đúng 0
Bình luận (0)

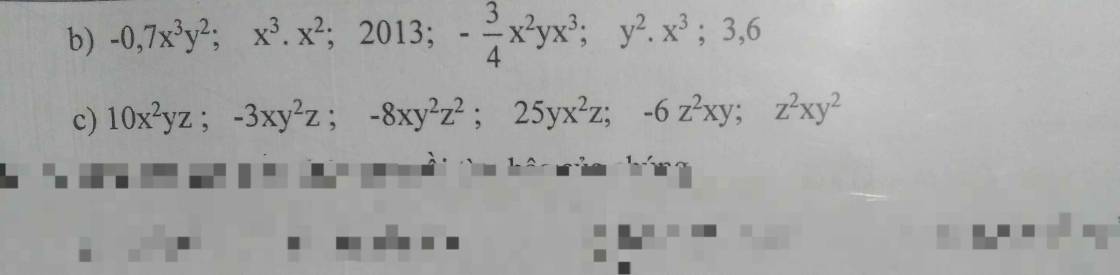 lamlàm cả 2 baibài chi tiết ạ e cảm ơn
lamlàm cả 2 baibài chi tiết ạ e cảm ơn
2:
a: Các đơn thức đồng dạng là \(2.5xy^3;-2xy^3\)
b: Các đơn thức đồng dạng là \(2013;3,6\)
\(-0.7x^3y^2;y^2\cdot x^3\)
c: Các đơn thức đồng dạng là \(10x^2yz;25yx^2z\)
\(-8xy^2z^2;z^2xy^2\)
Đúng 2
Bình luận (0)
a) Các đơn thức đồng dạng là:
\(2,5xy^3\) và \(-2xy^3\)
b) Các đơn thức của đồng dạng:
\(-0,7x^3y^2\) và \(y^2\cdot x^3\)
\(3,6\) và \(2013\)
c) Các đơn thứ đồng dạng là:
\(-8xy^2z^2\) và \(z^2xy^2\)
\(10x^2yz\) và \(25yx^2z\)
Đúng 1
Bình luận (0)
Làm bài 4 chi tiết 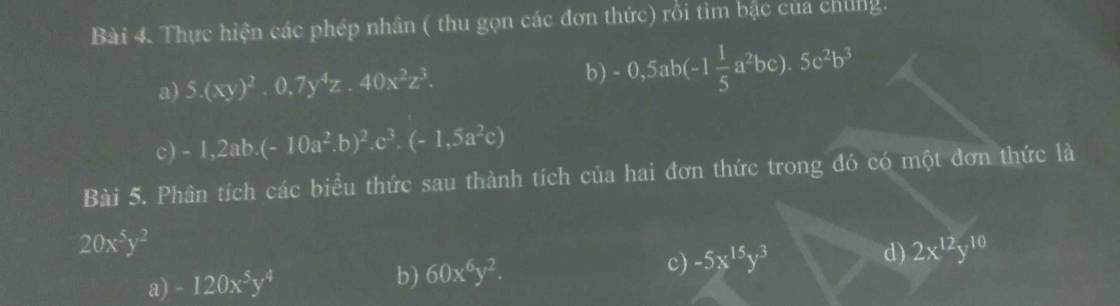 ạ
ạ
4:
a: \(=5x^2y^2\cdot\dfrac{7}{10}x^4y\cdot40x^2z^3\)
\(=\left(5\cdot\dfrac{7}{10}\cdot40\right)\left(x^2y^2\cdot x^4y\cdot x^2z^3\right)\)
\(=140x^8y^3z^3\)
Bậc là 8+3+3=14
b: \(=-\dfrac{1}{2}\cdot ab\cdot\dfrac{-4}{3}\cdot a^2bc\cdot5c^2b^3\)
\(=\left(\dfrac{1}{2}\cdot\dfrac{4}{3}\cdot5\right)\cdot ab\cdot a^2b\cdot c\cdot c^2b^3\)
\(=\dfrac{10}{3}a^3b^5c^3\)
Bậc là 11
c: \(=-1.2\cdot ab\cdot100a^4b^2\cdot c^3\cdot\left(-1.5\right)\cdot a^2c\)
\(=1.8\cdot100\cdot ab\cdot a^4b^2c^3\cdot a^2c\)
\(=180a^7b^3c^4\)
Bậc là 14
Đúng 3
Bình luận (0)
a) \(2x^2+A=4,5x^2\)
\(\Leftrightarrow A=4,5x^2-2x^2\)
\(\Leftrightarrow A=2,5x^2\)
b) \(-2,5m^2n+B=5m^2n\)
\(\Leftrightarrow B=5m^2n+2,5m^2n\)
\(\Leftrightarrow B=7,5m^2n\)
c) \(C-3,2ab^3=-11ab^3\)
\(\Leftrightarrow C=-11ab^3+3,2ab^3\)
\(\Leftrightarrow C=-7,8ab^3\)
d) \(-xyz^2-D=5xyz^2\)
\(\Leftrightarrow D=-xyz^2-5xyz^2\)
\(\Leftrightarrow D=-6xyz^2\)
Đúng 1
Bình luận (0)
a) \(2x^2+A=4,5x^2\)
\(\Rightarrow A=4,5x^2-2x^2\)
\(\Rightarrow A=2,5x^2\)
b) \(-2,5m^2n+B=5m^2n\)
\(\Rightarrow B=5m^2n-\left(-2,5m^2n\right)\)
\(\Rightarrow B=7,5m^2n\)
c) \(C-3,2ab^3=-11ab^3\)
\(\Rightarrow C=-11ab^3+3,2ab^3\)
\(\Rightarrow C=-7,8ab^3\)
d) \(-xyz^2-D=5xyz^2\)
\(\Rightarrow D=-xyz^2-5xyz^2\)
\(\Rightarrow D=-6xyz^2\)
#Ayumu
Đúng 1
Bình luận (0)
a: 2x^2+A=4,5x^2
=>A=4,5x^2-2x^2=2,5x^2
b: B-2,5m^2n=5m^2n
=>B=5m^2n+2,5m^2n=7,5m^2n
c: C-3,2ab^3=-11ab^3
=>C=-11ab^3+3,2ab^3=-7,8ab^3
d: -xyz^2-D=5xyz^2
=>D=-xyz^2-5xyz^2=-6xyz^2
Đúng 0
Bình luận (0)
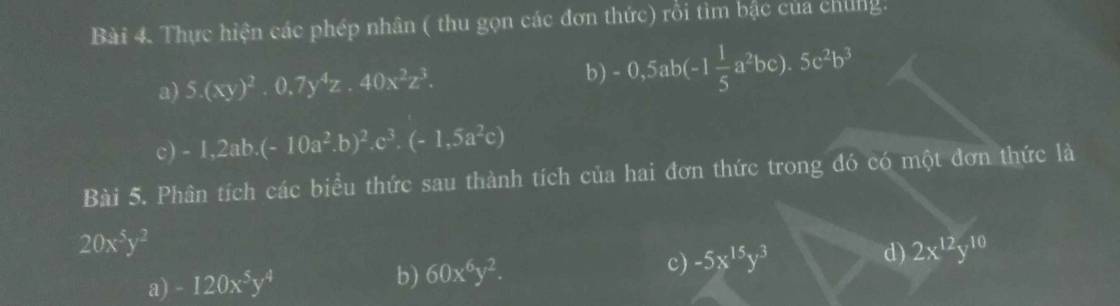 làm chi tiết ạ mik mới học nên cầm chi tiết nhất
làm chi tiết ạ mik mới học nên cầm chi tiết nhất
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
Đúng 0
Bình luận (0)
(2x-1)^2_(x+3)^2=0
\(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
\(=>\left(2x-1+x+3\right)\left(2x-1-x-3\right)=0\)
\(=>\left(3x+2\right)\left(x-4\right)=0\)
\(=>\left[{}\begin{matrix}3x+2=0\\x-4=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}3x=-2\\x=4\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=\dfrac{-2}{3}\\x=4\end{matrix}\right.\)
\(=>x\in\left\{\dfrac{-2}{3};4\right\}\)
Đúng 1
Bình luận (0)
\(\left(2x-1\right)^2-\left(x+3\right)^2=0\)(sửa đề)
\(\Leftrightarrow\left(2x-1-x-3\right)\left(2x-1+x+3\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)

mn oiw giup mik bai nay dc ko aj xin mn tai mik can gap
Bài 1. (a) Điều kiện: \(x\ne\pm1\).
Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)
\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)
\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)
\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)
\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)
Vậy: \(A=\dfrac{2}{1-x}\)
(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)
\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)
Vậy: \(x=\dfrac{1}{3}\)
Bài 2. (a) Phương trình tương đương với:
\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)
\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)
\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)
\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).
(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:
\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)
\(\Leftrightarrow2x+2+2x-2=2x^2+2\)
\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\varnothing\)
Đúng 2
Bình luận (0)

mn giup mik tu bai 1 den 3 dc ko aj plsss mn xin do
3:
1: =>15x-9x+6=45-10x+25
=>6x+6=-10x+70
=>16x=64
=>x=4
2: =>x^2+4x-16-16=0
=>x^2+4x-32=0
=>(x+8)(x-4)=0
=>x=4 hoặc x=-8
3: ĐKXĐ: x<>4; x<>-4
\(PT\Leftrightarrow\dfrac{x+4+\left(x+2\right)\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{5x-4}{\left(x-4\right)\left(x+4\right)}\)
=>x+4+x^2-2x-8=5x-4
=>x^2-x-4=5x-4
=>x^2-6x=0
=>x(x-6)=0
=>x=0 hoặc x=6
4: \(\Leftrightarrow5\left(4x+1\right)-x+2>=3\left(2x-3\right)\)
=>20x+5-x+2>=6x-9
=>19x+7>=6x-9
=>13x>=-16
=>x>=-16/13
Đúng 0
Bình luận (0)