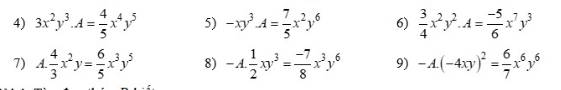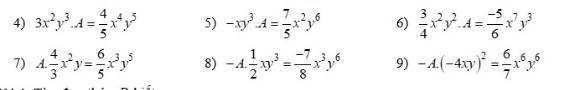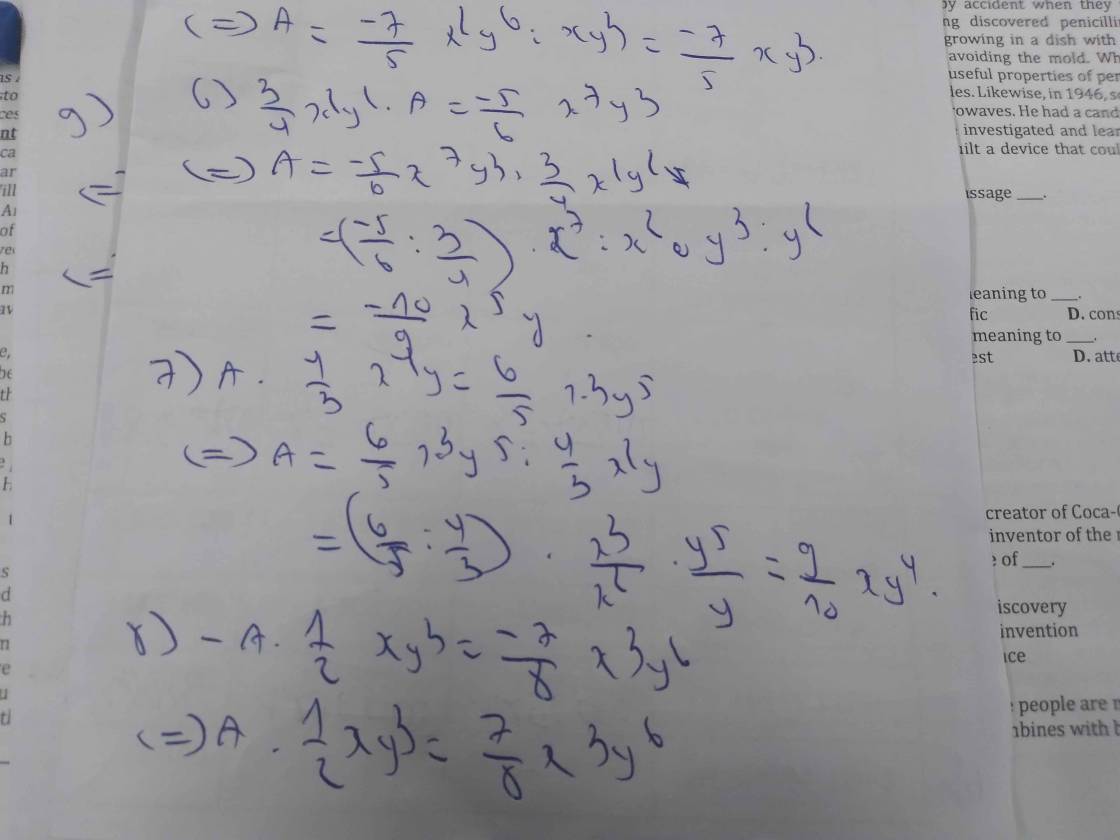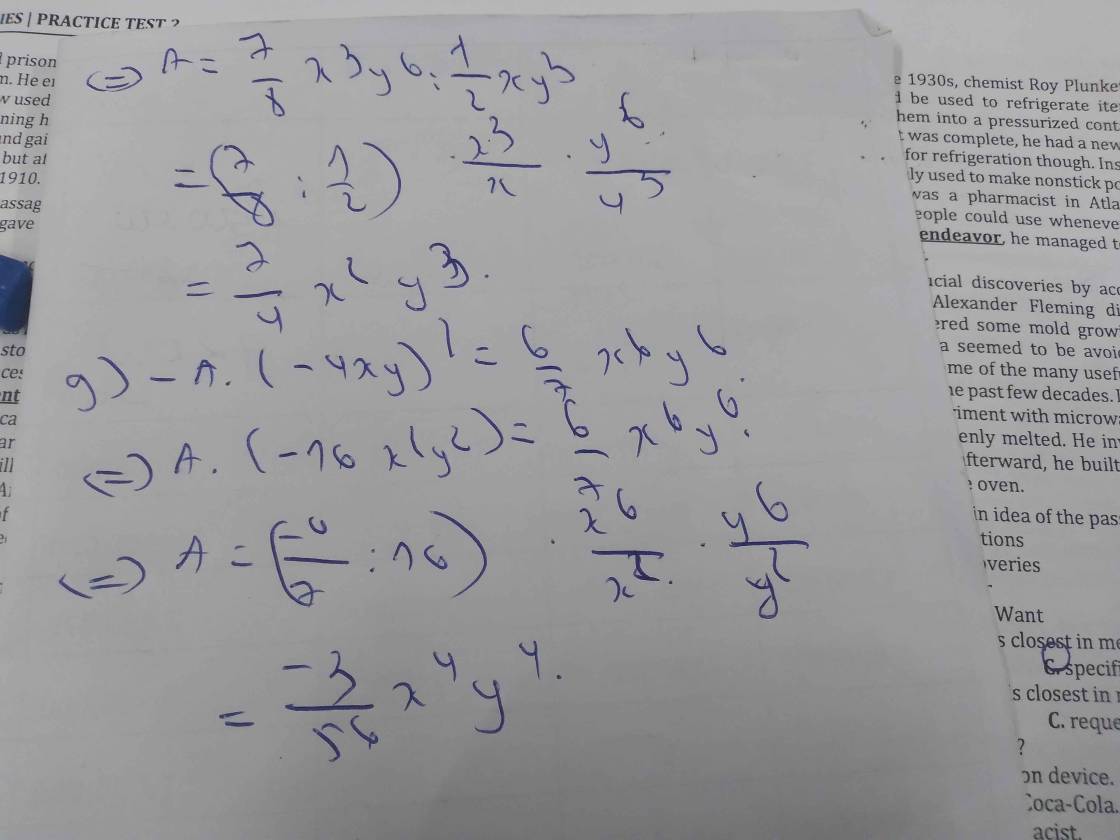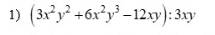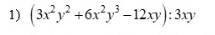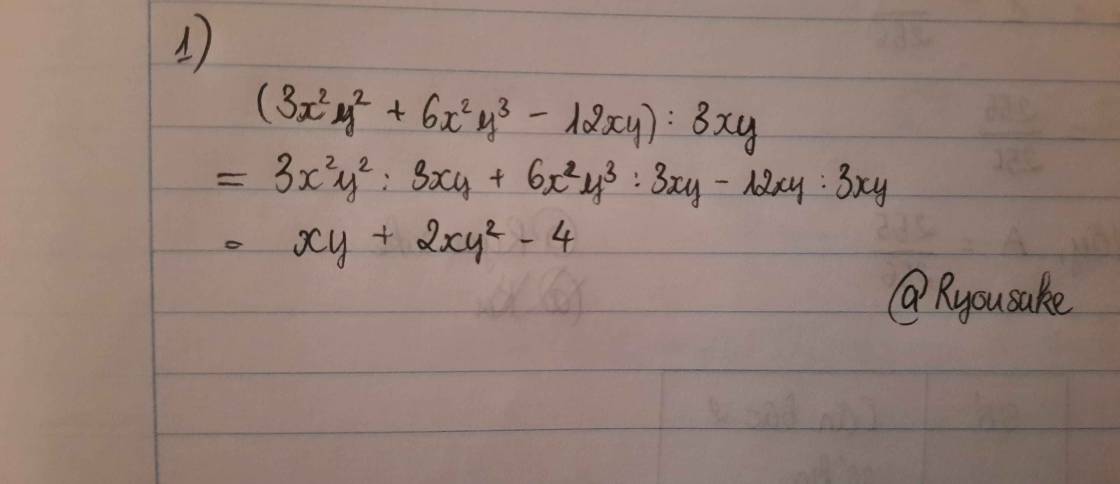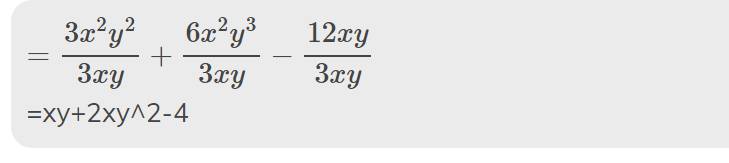Phép nhân và phép chia các đa thức

\(a,A=x\left(x+5\right)^3:\left(x+5\right)^2+x^2+x\)

\(=x\left(x+5\right)+x^2+x\)

\(=x^2+5x+x^2+x\)

\(=2x^2+6x\)

\(=2x\left(x+3\right)\)

Ta thấy: \(2x\left(x+3\right)⋮x+3\forall x\in Z\)

\(\Rightarrow A⋮x+3\forall x\in Z\)

\(b,B=x^4y^4:y^3x^3+xy+2\)

\(=xy+xy+2\)

\(=2xy+2\)

\(=2\left(xy+1\right)\)

Ta thấy: \(2\left(xy+1\right)⋮xy+1\forall x;y\in Z\)

\(\Rightarrow B⋮xy+1\forall x;y\in Z\)

\(c,C=xy\left(xy+y+1\right)^3:\left(xy+y+1\right)^2+xy\)

\(=xy\left(xy+y+1\right)+xy\)

\(=xy\left(xy+y+1+1\right)\)

\(=xy\left(xy+y+2\right)\)

Ta thấy: \(xy\left(xy+y+2\right)⋮xy+y+2\forall x;y\in Z\)

\(\Rightarrow C⋮xy+y+2\forall x;y\in Z\)

#\(Toru\)

`# \text {DNamNgV}`

`a)`

`A = x(x + 5)^3 \div (x + 5)^2 + x^2 + x`

`= x(x + 5) + x^2 + x`

`= x^2 + 5x + x^2 + x`

`= 2x^2 + 6x`

`= 2x(x + 3)`

Vì `2x(x + 3) \vdots (x + 3)`

`=> A=x(x + 5)^3 \div (x + 5)^2 + x^2 + x \vdots x + 3`

`b)`

`B=x^4y^4 \div y^3x^3 + xy + 2`

`= (x^4 \div x^3)(y^4 \div y^3) + xy + 2`

`= xy + xy + 2`

`= 2xy + 2`

`= 2(xy + 1)`

Vì `2(xy + 1) \vdots xy + 1`

`=> B =x^4y^4 \div y^3x^3 + xy + 2 \vdots xy + 1`

`c)`

`C = xy(xy + y + 1)^3 \div (xy + y + 1)^2 + xy`

`= xy(xy + y + 1) + xy`

`= xy(xy + y + 1 + 1)`

`= xy(xy + y + 2)`

Vì `xy(xy + y + 2) \vdots xy + y + 2`

`=> C = xy(xy + y + 1)^3 \div (xy + y + 1)^2 + xy \vdots xy + y + 2.`

4) \(3x^2y^3\cdot A=\dfrac{4}{5}x^4y^5\)

\(\Rightarrow A=\dfrac{4}{5}x^4y^5:3x^2y^3\)

\(\Rightarrow A=\dfrac{4}{15}x^2y^2\)

5) \(-xy^3\cdot A=\dfrac{7}{5}x^2y^6\)

\(\Rightarrow A=\dfrac{7}{5}x^2y^6:\left(-xy^3\right)\)

\(\Rightarrow A=-\dfrac{7}{5}xy^3\)

6) \(\dfrac{3}{4}x^2y^2\cdot A=\dfrac{-5}{6}x^7y^3\)

\(\Rightarrow A=-\dfrac{5}{6}x^7y^3:\dfrac{3}{4}x^2y^2\)

\(\Rightarrow A=-\dfrac{10}{9}x^5y\)

7) \(A\cdot\dfrac{4}{3}x^2y=\dfrac{6}{5}x^3y^5\)

\(\Rightarrow A=\dfrac{6}{5}x^3y^5:\dfrac{4}{3}x^2y\)

\(\Rightarrow A=\dfrac{9}{10}xy^4\)

8) \(-A\cdot\dfrac{1}{2}xy^3=\dfrac{-7}{8}x^3y^6\)

\(\Rightarrow A\cdot\dfrac{-1}{2}xy^3=-\dfrac{7}{8}x^3y^6\)

\(\Rightarrow A=-\dfrac{7}{8}x^3y^6:\left(-\dfrac{1}{2}xy^3\right)\)

\(\Rightarrow A=\dfrac{7}{4}x^2y^3\)

9) \(-A\cdot\left(-4xy\right)^2=\dfrac{6}{7}x^6y^6\)

\(\Rightarrow-A\cdot16x^2y^2=\dfrac{6}{7}x^6y^6\)

\(\Rightarrow-A=\dfrac{6}{7}x^6y^6:16x^2y^2\)

\(\Rightarrow-A=\dfrac{3}{56}x^4y^4\)

\(\Rightarrow A=-\dfrac{3}{56}x^4y^4\)

#Urushi☕

\(=\dfrac{3x^2y^2}{3xy}+\dfrac{6x^2y^3}{3xy}-\dfrac{12xy}{3xy}\)

=xy+2xy^2-4

Lời giải:

$(3x^2y^2+6x^2y^3-12xy):(3xy)$

$=\frac{3x^2y^2}{3xy}+\frac{6x^2y^3}{3xy}-\frac{12xy}{3xy}$

$=xy+2xy^2-4$

16:

a:A=xy(x+y)-x^2y(1+y)

=x^2y+xy^2-x^2y-x^2y^2

=xy^2-x^2y^2

=y^2(x-x^2)

Khi x=1 và y=2 thì A=2^2(1-1^2)=0

b: B=x(x^2+y)-y(x+y^2)-x(x^2+y^2)

=x^3+xy-xy-y^3-x^3-y^3

=-2y^3

Khi y=1 thì B=-2*1^3=-2

c: C=xy(x+z)-y(x^2-x)-z(xy+x)

=x^2y+xyz-x^2y+xy-xyz-xz

=xy-xz

=x(y-z)

Khi x=2 và y=1 thì C=2(1-z)

5x(3-2x)+5(x-4)=6-4x

=>15x-10x^2+5x-20=6-4x

=>-10x^2+20x-20-6+4x=0

=>-10x^2+24x-26=0

=>5x^2-12x+13=0

=>x^2-12/5x+13/5=0

=>x^2-2*x*6/5+36/25+29/25=0

=>(x-6/5)^2+29/25=0(vô lý)

Bước 1: Mở ngoặc và kết hợp các thành phần tương tự: 5x(3-2x) + 5(x-4) = 6-4x 15x - 10x^2 + 5x - 20 = 6 - 4x

Bước 2: Đưa tất cả các thành phần về cùng một phía và biến đổi phương trình: 15x - 10x^2 + 5x - 20 + 4x - 6 = 0 -10x^2 + 24x - 26 = 0

Bước 3: Giải phương trình bậc hai. Có thể sử dụng công thức nghiệm của phương trình bậc hai hoặc sử dụng máy tính hoặc ứng dụng để giải phương trình này. Kết quả là: x ≈ 0.642 hoặc x ≈ 2.558

Vậy, giá trị của x là khoảng 0.642 hoặc 2.558.

`#040911`

`a)`

\(7.(x-9)-5.(6-x)=-6+11x\)

`<=> 7x - 63 - 30 + 5x = 11x - 6`

`<=> 7x + 5x - 11x = 63 + 30 - 6`

`<=> (7 + 5 - 11)x = 87`

`<=> x = 87`

Vậy, `x = 87.`

=>7x-63-30+5x=11x-6

=>12x-93=11x-6

=>x=-6+93=87

9:

M=A+B

\(=\dfrac{1}{3}x^2y^2-xyz+3xy-5+5xyz+3xy+2x-\dfrac{1}{3}x^2y^2\)

\(=4xyz+6xy+2x-5\)

Bậc là 3

=>C

Câu 10:

N=A-B

\(=-3x^3y^2-x^2y+3xy-1+x^2y+3x^3y^2-3xy+3\)

=2

=>Bậc là 0

=>A

Câu 11:

\(2A-B=-2x^2y^2-2x^2y+8-3x^2y^2-2xy+2\)

=-5x^2y^2-2x^2y-2xy+10

=>B

12:

M=B-A

\(=-x^2y^3+2x^2y-6x+4+x^2y-4x^2y^3-2\)

=-5x^2y^3+3x^2y-6x+2

=>Chọn D

13:

\(A+B=-x^2y+4xy+2x-1+2x^2y-3x+2-4xy\)

=x^2y-x+1

KHi x=-1 và y=0,5 thì A+B=(-1)^2*0,5+1+1=2,5

=>D

14:
A+B=3/2x^2y-2/3xy^2+xy+2+2/3xy^2-3/2x^2y+5

=xy+7

Khi y=2 thì A+B=3

=>2x+7=3

=>x=-2

=>Chọn C

9: M=1/3x^2y^2-xyz+3xy-5+5xyz+3xy+2x-1/3x^2y^2

=4xyz+6xy+2x-5

=>Chọn C

8:

M-N

=3xy^2-2x^2y-1+x^2y+2xy-2

=3xy^2-x^2y+2xy-3

=>Chọn C

7:

A-B

=3xy^2-2x^2y+3xy-1+2x^2y-xy^2+2xy-2

=2xy^2+5xy-3

=>Chọn D

6:

M+N

\(=x^2y^2z-x^2y+2xy-x^2y^2z+2x^2y-3xy+2\)

=x^2y-xy+2

=>Chọn B

5:
A+B

=3x^2y^2-xy+3-x^2y^2+2xy-3

=2x^2y^2+xy

=>Chọn A