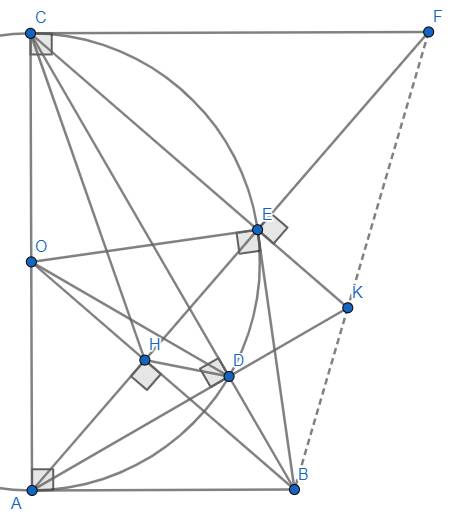
Cho dg tròn tâm O ĐIỂM M năng ngoài đường tròn kẻ tiếp tuyến MA MB với đường tròn a CM i là Trung điểm AB ( với i là giao điểm của MO và AB) b CM OI = 1 phần 2 AD tính OI khi AD = 6cm với BD là đường kính đường tròn tâm O
Ôn tập Đường tròn
a: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại I và I là trung điểm của AB
b: Xét ΔBAD có BO/BD=BI/BA
nên OI//AD
=>OI/AD=BO/BD=1/2
=>OI=1/2AD
Khi AD=6 thì OI=1/2*6=3cm
Đúng 0
Bình luận (0)
Cho góc xAy = 60 độ, đường tròn (O) tiếp xúc với tia Ax tại B, tiếp xúc với tia Ay tại C. Trên cung nhỏ BC của đường tròn (O) lấy điểm M, gọi D, E, F lần lượt là hình chiếu của điểm M trên BC, CA, AB. a. Chứng minh CDME là tứ giác nội tiếp b. Tính số đo góc EDF c. Chứng minh rằng MD^2= ME*MF
a: góc CEM+góc CDM=180 độ
=>CEMD nội tiếp
b: góc EDM=góc ECM
góc FDM=góc FBM=góc ABM
=>góc EDF=góc ACM+góc ABM=60 độ
Đúng 0
Bình luận (0)
cho (O;R) từ A nằm ngoài đường tròn kẻ 2 tiếp tuyến AB và AC .Qua B kẻ đường thẳng song song với AO cắt (O) tại M .AM cắt (O) tại N. BN cắt AO tại I ,AO cắt BC tại K a) ABOC nội tiếp b)IA^2 = IN . IB
cho (O;R) từ A nằm ngoài đường tròn kẻ 2 tiếp tuyến AB và AC .Qua B kẻ đường thẳng song song với AO cắt (O) tại M .AM cắt (O) tại N. BN cắt AO tại I ,AO cắt BC tại K a) ABOC nội tiếp b)IA^2 = IN . IB
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔIAN và ΔIBA có
góc IAN=góc IBA
góc AIN chung
=>ΔIAN đồng dạng với ΔIBA
=>IA^2=IN*IB
Đúng 0
Bình luận (1)
Cho △ABC có 3 góc nhọn nội tiếp (O) (AB<AC). Các đường cao BM và CN cắt nhau tại H. Gọi P là giao điểm của MN và BC. Đường thẳng AP cắt (O) tại K,Gọi I là trung điểm của BC.Chứng minh H,K,I thẳng hàng.thank m,n
ΔPKN đồng dạng với ΔPMA
=>góc PKN=góc PMH
=>AKNM nội tiếp
mà góc ANH=góc AMH=90 độ
nên ANHM nội tiếp đường tròn đường kính AH
=>góc AKH=góc ANH
=>AK vuông góc KH
Kẻ đường kính AI' của (O)
=>I'K vuông góc AK
=>K,H,I' thẳng hàng
AC vuông góc CI' AB vuông góc BI'
=>CI'//BH và BI'//CH
=>BHCI' là hình bình hành
=>K,H,I thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB <AC) vẽ đường tròn (O) đường kính AC , đường tròn (O) cắt BC tại D .Vẽ tiếp tuyến BE của (o) ( E là tiếp điểm) .BO cắt AE tại H
a) Chứng Minh : Tứ giác OB vuông AE và BH.BO=BD.BC
Chứng minh DHOC là tứ giác nội tiếp và BHD=OHC
Giup mk ạ =((((
a: Xét (O) có
BA,BE là tiếp tuyến
=>BA=BE
mà OA=OE
nên OB là trung trực của AE
=>OB vuông góc AE
=>BH*BO=BA^2
ΔABC vuông tại A có AD vuông góc BC
nên BD*BC=BA^2
=>BH*BO=BD*BC
b: BH*BO=BD/BC
=>BH/BC=BD/BO
=>góc BHD=góc BCO
=>góc DHO+góc DCO=180 độ
=>DHOC nội tiếp
Đúng 1
Bình luận (0)
giúp em cau c voi cac thầy ơi... em cảm ơn nhieu ạ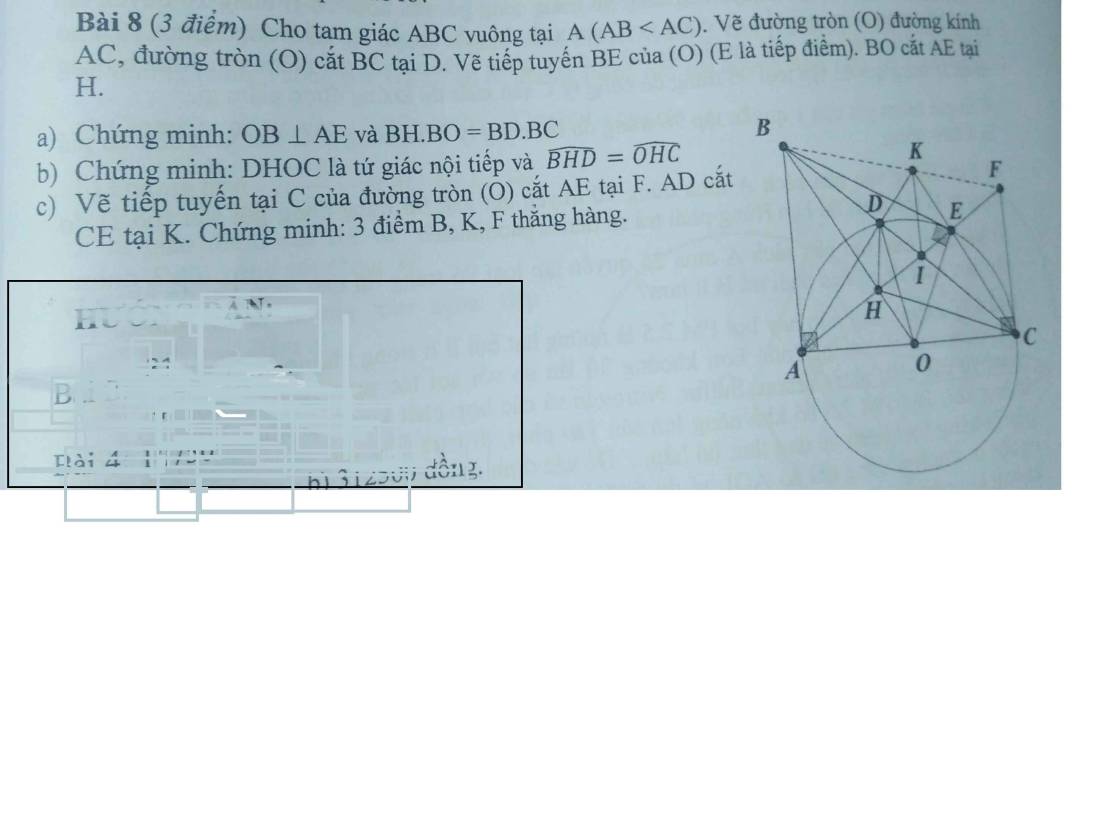
Cho đường tròn tâm (O) và điểm K nằm ngoài đường tròn. Từ K kẻ các tiếp tuyến KA,KB đến (O). Một đường thẳng qua K cắt (O) tại C,D sao cho C nằm giữa K và D, đồng thời hai điểm O, A nằm khác phía so với CD.a) CM tứ giác OAKB nội tiếp và KA2 KC.KDb) Gọi M là giao điểm của đoạn OK và AB. CM góc KMCKDOc) Kẻ đường kính AI của (O). Gọi G, N lần lượt là giao điểm của OK với các đoạn CI, DI. Chứng minh tứ giác AMND nội tiếp và OGON.
Đọc tiếp
Cho đường tròn tâm (O) và điểm K nằm ngoài đường tròn. Từ K kẻ các tiếp tuyến KA,KB đến (O). Một đường thẳng qua K cắt (O) tại C,D sao cho C nằm giữa K và D, đồng thời hai điểm O, A nằm khác phía so với CD.
a) CM tứ giác OAKB nội tiếp và KA2= KC.KD
b) Gọi M là giao điểm của đoạn OK và AB. CM góc KMC=KDO
c) Kẻ đường kính AI của (O). Gọi G, N lần lượt là giao điểm của OK với các đoạn CI, DI. Chứng minh tứ giác AMND nội tiếp và OG=ON.
a: góc OAK+góc OBK=90+90=180 độ
=>OAKB nội tiếp
Xét ΔKAC và ΔKDA có
góc KAC=góc KDA
góc AKC chung
=>ΔKAC đồng dạng với ΔKDA
=>KA^2=KC*KD
b: Xét (O) có
KA,KB là tiếp tuyến
=>KA=KB
=>OK là trung trực của AB
=>KM*KO=KA^2=KC*KD
=>KM/KD=KC/KO
=>ΔKMC đồng dạng với ΔKDO
=>góc KMC=góc KDO
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB AC. Trên nửa mặt phẳng bờ là đường thẳng AC chứa điểm B vẽ nửa đường tròn (O) đường kính AC, nửa đường tròn này cắt BC tại D. Vẽ tiếp tuyến BE của nửa đường tròn (O)(với E là tiếp điểm, E khác 4). BO cắt AE tại điểm H .
a) Chứng minh BAOE nội tiếp và BH.BO BD.BC.
b) Chứng minh DHOC là tứ giác nội tiếp và BHDOHC.
c) Tiếp tuyến tại C của nửa đường tròn (O) cắt AE tại F, AD cắt CE tại K. Chứng minh ba điểm B,K,F thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB < AC. Trên nửa mặt phẳng bờ là đường thẳng AC chứa điểm B vẽ nửa đường tròn (O) đường kính AC, nửa đường tròn này cắt BC tại D. Vẽ tiếp tuyến BE của nửa đường tròn (O)(với E là tiếp điểm, E khác 4). BO cắt AE tại điểm H . a) Chứng minh BAOE nội tiếp và BH.BO = BD.BC. b) Chứng minh DHOC là tứ giác nội tiếp và BHD=OHC. c) Tiếp tuyến tại C của nửa đường tròn (O) cắt AE tại F, AD cắt CE tại K. Chứng minh ba điểm B,K,F thẳng hàng.
a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O). Biết BC = 2cm , A =45^ . a. Tính diện tích hình tròn (O). b. Tính diện tích hình viên phân giới hạn bởi dây BC và cung nhỏ BC. C,Xác định vị trí của điểm A để diện tích tam giác ABC là lớn nhất. Tính diện tích lớn nhất đó .. Giúp tớ với
a: góc BOC=2*góc A=90 độ
=>OB^2+OC^2=BC^2
=>2*R^2=2^2=4
=>R=căn 2
\(S_{\left(O\right)}=R^2\cdot pi=2pi\left(cm^2\right)\)
b: \(S_{q\left(BOC\right)}=pi\cdot2\cdot\dfrac{90}{360}=\dfrac{1}{2}\cdot pi\left(cm^2\right)\)
\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2=1\)
=>\(S_{viênphân}=\dfrac{1}{2}\cdot3.14-1=0.57\left(cm^2\right)\)
Đúng 0
Bình luận (1)