Ôn tập cuối năm phần hình học

\(a,BD=\sqrt{AB^2+AD^2}=\sqrt{5^2+12^2}=13\left(cm\right)\left(pytago\right)\)

Áp dụng HTL tam giác

\(\left\{{}\begin{matrix}AB^2=BH\cdot BD\\AD^2=DH\cdot BD\\AH^2=BH\cdot HD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BD}=\dfrac{25}{13}\left(cm\right)\\DH=\dfrac{AD^2}{BD}=\dfrac{144}{13}\left(cm\right)\\AH=\sqrt{\dfrac{25\cdot144}{13^2}}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)

\(b,\widehat{MAN}=\widehat{ANM}=\widehat{AMN}\left(=90^0\right)\\ \Rightarrow AMHN.là.hcn\\ \Rightarrow AH=MN=\dfrac{60}{13}\left(cm\right)\)

\(c,\) Vì \(AMHN\) là hcn nên \(\widehat{MAH}=\widehat{ANM}\)

Mà \(\widehat{MAH}=\widehat{ADB}\left(cùng.phụ.\widehat{HAD}\right)\)

\(\Rightarrow\widehat{ANM}=\widehat{ADB}\)

\(\left\{{}\begin{matrix}\widehat{ANM}=\widehat{ADB}\\\widehat{BAD}.chung\end{matrix}\right.\Rightarrow\Delta AMN\sim\Delta ADB\left(g.g\right)\\ \Rightarrow\dfrac{AM}{AD}=\dfrac{AN}{AB}\Rightarrow AM\cdot AB=AN\cdot AD\)

a/ Xét △AHB và △DAB ta được: △AHB đồng dạng △DAB (g.g) (Tự chứng minh)

\(\Rightarrow\dfrac{AH}{AD}=\dfrac{HB}{AB}=\dfrac{AB}{BD}\left(a\right)\) 

Áp dụng định lí Pytago vào △ADB được: \(BD=\sqrt{12^2+5^2}=13\left(cm\right)\). Thay vào (a) được:

\(\dfrac{AH}{AD}=\dfrac{HB}{AB}=\dfrac{AB}{13}\) hay \(\dfrac{AH}{12}=\dfrac{HB}{5}=\dfrac{5}{13}\)

 \(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{5.12}{13}\approx4,62\left(cm\right)\\HB=\dfrac{5^2}{13}\approx1,92\left(cm\right)\\HD=13-1,92=11,08\left(cm\right)\end{matrix}\right.\)

==========

b/ \(\begin{matrix}\hat{A}=90\text{°}\\\hat{AMH}=90\text{°}\\\hat{ANH}=90\text{°}\end{matrix}\) ⇒ AMHN là hình chữ nhật ⇒ \(AH=MN\approx4,92\left(cm\right)\)

==========

c/ Ta có: △AMN = △HNA (c.g.c) (Tự chứng minh)

Ta cũng có: △HNA đồng dạng △AHB (g.g) (Tự chứng minh) ⇒ △HNA đồng dạng △DAB (cùng đồng dạng △AHB) ⇒ △AMN đồng dạng △DAB

Vậy: \(\dfrac{AM}{AN}=\dfrac{AB}{AD}\) hay \(AM.AD=AN.AB\left(đpcm\right)\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(AH^2=HB\cdot HC\)

hay HC=10,24(cm)

\(\Leftrightarrow BC=35,24\left(cm\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{BH\cdot BC}=\sqrt{25\cdot35.24}=\sqrt{881}\left(cm\right)\\AC=\sqrt{CH\cdot BC}=\sqrt{10.24\cdot35.24}=\sqrt{360.8576}\left(cm\right)\end{matrix}\right.\)

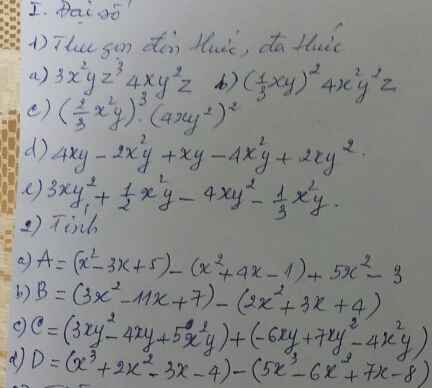
Bài 2: 

a: Ta có: \(A=\left(x^2-3x+5\right)-\left(x^2+4x-1\right)+5x^2-3\)

\(=x^2-3x+5-x^2-4x+1+5x^2-3\)

\(=5x^2-7x+3\)

bạn tách nhỏ câu hỏi ra, dài thế không ai lm hết đâu

a:Xét hình thang ABCD có 

M là trung điểm của AD

MN//AB//CD

Do đó: N là trung điểm của BC

Xét ΔDAB có 

M là trung điểm của AD

ME//AB

Do đó: E là trung điểm của BD

Xét ΔABC có 

N là trung điểm của BC

NF//AB

Do đó: F là trung điểm của AC

a: Xét ΔAMC vuông tại M có MH là đường cao ứng với cạnh huyền AC

nên \(MC^2=AC\cdot HC\)

a: Xét ΔABD vuông tại A và ΔMAD vuông tại M có 

\(\widehat{MDA}\) chung

Do đó: ΔABD\(\sim\)ΔMAD

a: Xét ΔHNB vuông tại N và ΔHMC vuông tại M có 

\(\widehat{NHB}=\widehat{MHC}\)

Do đó: ΔHNB\(\sim\)ΔHMC

Suy ra: \(\dfrac{HB}{HC}=\dfrac{HN}{HM}\)

hay \(\dfrac{HB}{HN}=\dfrac{HC}{HM}\)

Xét ΔHBC và ΔHNM có 

\(\dfrac{HB}{HN}=\dfrac{HC}{HM}\)

\(\widehat{BHC}=\widehat{NHM}\)

Do đó: ΔHBC\(\sim\)ΔHNM

Suy ra: \(\dfrac{BC}{NM}=\dfrac{HB}{HN}=\dfrac{HC}{HM}\)

\(\Leftrightarrow\dfrac{MN}{BC}=\dfrac{HN+HM}{HB+HC}\)