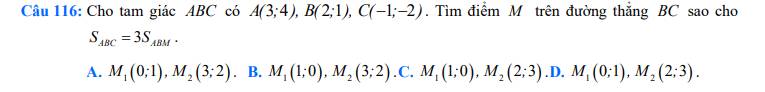Ôn tập cuối năm môn Hình học

BM: 2x-y+1=0

=>M(x;2x+1)

CN: x+y-4=0

=>C(-y+4;y)

Theo đề, ta có: -y+4+(-2)=2x và y+3=2(2x+1)

=>4x+2-y-3=0 và 2x+y-2=0

=>4x-y-1=0 và 2x+y-2=0

=>x=1/2 và y=1

=>M(1/2;2); C(3;1)

Tọa độ G là:

2x-y+1=0 và x+y-4=0

=>x=1 và y=3

G(1;3); B(x;y); M(1/2;2)

Theo đè, ta có; vecto BG=2/3vecto BM

=>1-x=2/3x và 3-y=2/3(2-y)

=>1-5/3x=0 và 3-y-4/3+2/3y=0

=>x=3/5 và y=5

=>B(3/5;5); A(-2;3); C(3;1)

vecto BA=(-2,6;-2)

=>VTPT là (2;2,6)=(10;13)

Phương trình BA là:

10(x+2)+13(y-3)=0

=>10x+20+13y-39=0

=>10x+13y-19=0

vecto AC=(5;-2)

=>VTPT là (2;5)

Phương trình AC là:

2(x-3)+5(y-1)=0

=>2x-6+5y-5=0

=>2x+5y-11=0

vecto BC=(2,4;-4)

=>VTPT là (5;3)

Phương trình BC là

5(x-3)+3(y-1)=0

=>5x-15+3y-3=0

=>5x+3y-18=0

2:

a: vecto AC=(4;-3)

=>VTPT là (3;4)

Phương trình AC là:

3(x+2)+4(y-2)=0

=>3x+6+4y-8=0

=>3x+4y-2=0

b: PTTQ của BH nhận vecto AC làm vecto pháp tuyến

=>VTPT là (4;-3)

Phương trình BH là:

4(x+4)+(-3)(y+1)=0

=>4x+16-3y-3=0

=>4x-3y+13=0

c: Tọa độ H là:

4x-3y+13=0 và 3x+4y-2=0

=>x=-46/25 và y=47/25

Ta có B(a;2-a) ; C(b;8-b)

Để tam giác ABC vuông cân tại A

\(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{AB}=\overrightarrow{0}\\\overrightarrow{AC}=\overrightarrow{AB}\end{matrix}\right.\) bạn thay vào giải hpt bằng p2 thế nhé 

a: vecto AB=(-7;1)

vecto AC=(1;-3)

vecto BC=(8;-4)

b: \(AB=\sqrt{\left(-7\right)^2+1^2}=5\sqrt{2}\)

\(AC=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)

\(BC=\sqrt{8^2+\left(-4\right)^2}=\sqrt{80}=4\sqrt{5}\)

Số tam giác lập được là: \(C^2_6\cdot1=15\left(tamgiác\right)\)

Chọn C

\(\overrightarrow{BC}=\left(-3;-3\right)\)

\(\overrightarrow{BM}=\left(x_M-2;y_M-1\right)\)

S_ABC = 3S_ABM --> BC = 3BM

TH1: \(\overrightarrow{BC}=3\overrightarrow{BM}\) --> -3 = 3(x_M - 2) và -3 = 3(y_M - 1)

--> x_M = 1 và y_M = 0 --> M(1;0)

TH2: \(\overrightarrow{BC}=-3\overrightarrow{BM}\) --> -3 = -3(x_M - 2) và -3 = -3(y_M - 1)

--> x_M = 3 và y_M = 2 --> M(3;2)

Vậy chọn B.

Ta có:

\(cotA=\dfrac{cosA}{sinA}=\dfrac{\dfrac{b^2+c^2-a^2}{2bc}}{\dfrac{a}{2R}}=R.\dfrac{b^2+c^2-a^2}{abc}\)

Tương tự: \(cotB=R.\dfrac{a^2+c^2-b^2}{abc}\) ; \(cotC=R.\dfrac{a^2+b^2-c^2}{abc}\)

\(\Rightarrow cotA+cotB+cotC=\dfrac{R}{abc}\left(b^2+c^2-a^2+a^2+c^2-b^2+a^2+b^2-c^2\right)\)

\(=\dfrac{R}{abc}.\left(a^2+b^2+c^2\right)\)

Mà \(S=\dfrac{abc}{4R}\Rightarrow\dfrac{R}{abc}=\dfrac{1}{4S}\)

\(\Rightarrow cotA+cotB+cotC=\dfrac{a^2+b^2+c^2}{4S}\)

\(A=\dfrac{1}{2}+\dfrac{\sqrt{2}}{2}-1-\dfrac{\sqrt{3}}{3}=\dfrac{3+3\sqrt{2}-6-2\sqrt{3}}{6}\)

\(=\dfrac{3\sqrt{2}-3-2\sqrt{3}}{6}\)

\(B=\left(\dfrac{1}{2}+\dfrac{1}{3}\right):\left(1-\dfrac{1}{3}\right)=\dfrac{5}{6}:\dfrac{2}{3}=\dfrac{5}{6}\cdot\dfrac{3}{2}=\dfrac{15}{12}=\dfrac{5}{4}\)