Chương II : Tam giác

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

mà CQ//AM

nên CQ\(\perp\)CB

Ta có: \(\widehat{ACQ}+\widehat{ACB}=\widehat{QCB}=90^0\)

\(\widehat{ABC}+\widehat{AQC}=90^0\)(ΔQCB vuông tại C)

mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)

nên \(\widehat{ACQ}=\widehat{AQC}\)

=>AQ=AC

mà AB=AC

nên AQ=AB

c: Vì QC\(\perp\)CB tại C

nên ΔQCB vuông tại C

=>\(\widehat{QBC}+\widehat{CQA}=90^0\)

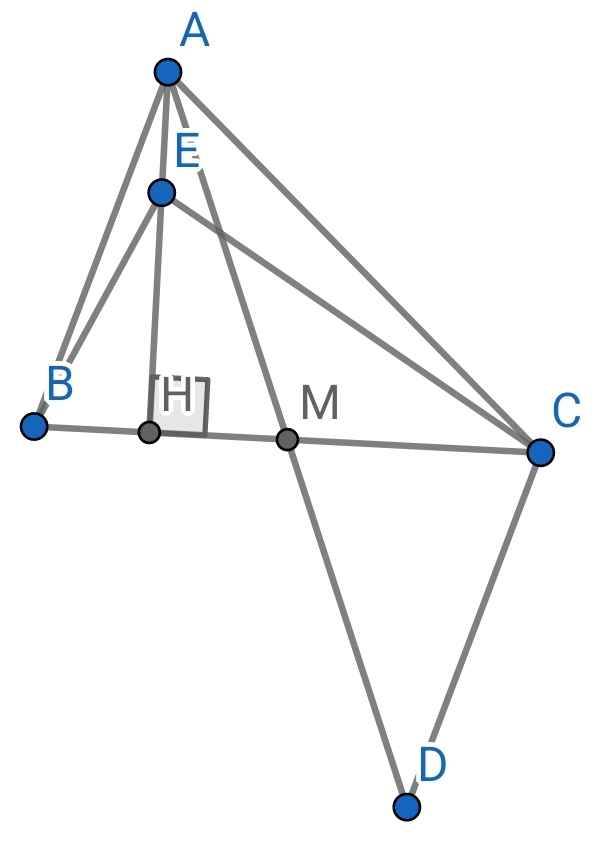
a) Do M là trung điểm của BC (gt)

⇒ MB = MC

Xét ∆AMB và ∆DMC có:

AM = DM (gt)

∠AMB = ∠DMC (đối đỉnh)

MB = MC (cmt)

⇒ ∆AMB = ∆DMC (c-g-c)

⇒ AB = CD

Mà AC > AB (gt)

⇒ AC > CD

∆ACD có:

AC > CD (cmt)

⇒ ∠ADC > ∠DAC

Do ∆AMB = ∆DMC (cmt)

⇒ ∠MAB = ∠MDC (hai góc tương ứng)

⇒ ∠MAB = ∠ADC

Mà ∠ADC > ∠DAC (cmt)

⇒ ∠MAB > ∠MAC

b) Do AC > AB (gt)

AH là đường vuông góc hạ từ A đến BC

⇒ HC > HB (đường xiên nào lớn hơn thì hình chiếu lớn hơn)

Do E nằm giữa A và H (gt)

⇒ EH là đường vuông góc hạ từ E đến BC

Mà HC > HB (cmt)

⇒ EC > EB (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)

Bài 3:

a: Ta có: \(\widehat{ABC}+\widehat{C}=90^0\)(ΔABC vuông tại A)

\(\widehat{CED}+\widehat{C}=90^0\)(ΔCDE vuông tại D)

Do đó: \(\widehat{ABC}=\widehat{CED}\)

c: Xét tứ giác ABDE có

\(\widehat{EAB}+\widehat{EDB}=90^0+90^0=180^0\)

=>ABDE là tứ giác nội tiếp

=>\(\widehat{DBE}=\widehat{DAE}=45^0\)

Xét ΔDBE vuông tại D có \(\widehat{DBE}=45^0\)

nên ΔDBE vuông cân tại D

=>DB=DE

Bài 4:

a: Ta có: \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}\)

\(\widehat{ACE}+\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)

Xét ΔABD và ΔACE có

\(\widehat{ABD}=\widehat{ACE}\)

AB=AC

\(\widehat{BAD}\) chung

Do đó:ΔABD=ΔACE

=>AD=AE

=>ΔADE cân tại A

b: ta có: AE+EB=AB

AD+DC=AC

mà AE=AD và AB=AC

nên EB=DC

c: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)

nên ΔOBC cân tại O

=>OB=OC

ta có: ΔAEC=ΔADB

=>EC=BD

Ta có: OE+OC=EC

OD+OB=BD

mà EC=BD và OC=OB

nên OE=OD

=>ΔOED cân tại O

Bài 2 : Tớ mới vẽ hình thôi ;-;

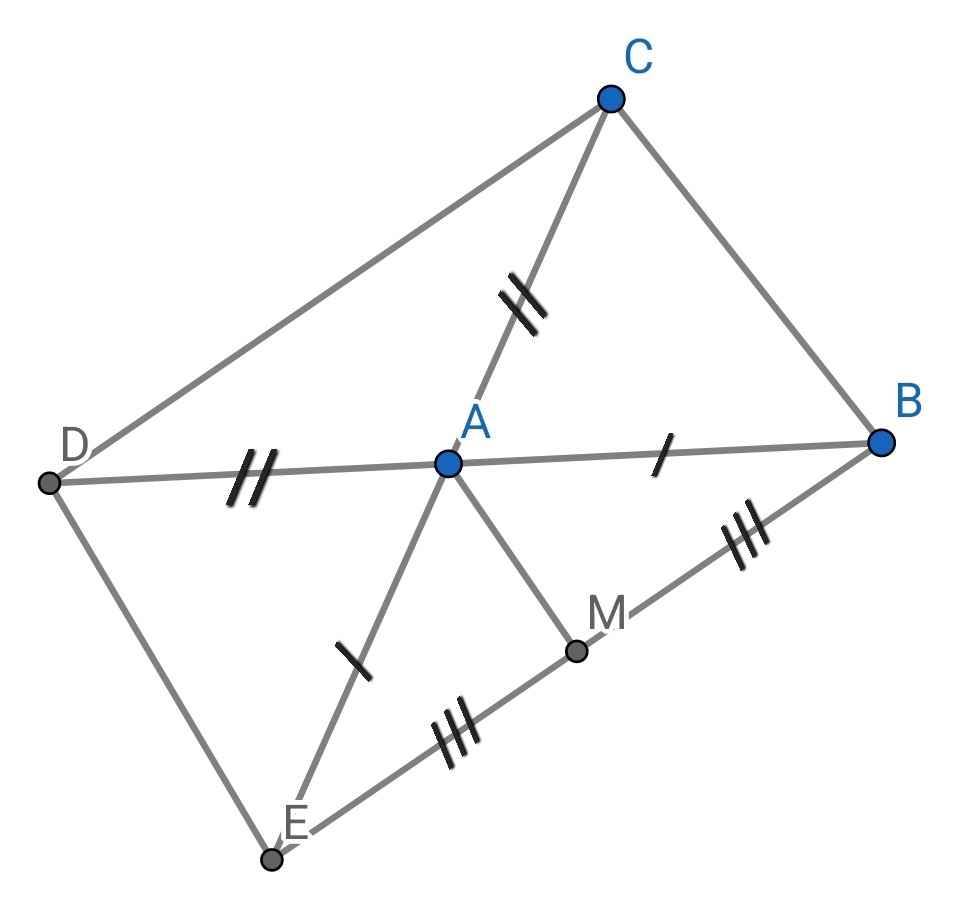 a) Xét ∆ABC và ∆AED có:

AB = AE (gt)

∠BAC = ∠DAE (đối đỉnh)

AC = AD (gt)

⇒ ∆ABC = ∆AED (c-g-c)

⇒ BC = DE (hai cạnh tương ứng)

b) ∆ACD có:

AC = AD (gt)

⇒ ∆ACD cân tại A

∆ABE có:

AB = AE (gt)

⇒ ∆ABE cân tại A

c) Do M là trung điểm của BE (gt)

⇒ MB = ME

Xét ∆ABM và ∆AEM có:

AB = AE (gt)

AM là cạnh chung

MB = ME (cmt)

⇒ ∆ABM = ∆AEM (c-c-c)

⇒ ∠AMB = ∠AME (hai góc tương ứng)

Mà ∠AMB + ∠AME = 180⁰ (kề bù)

⇒ ∠AMB = ∠AME = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BE

Giúp tớ câu 1 aa

Bài 1:

1: Xét ΔABC và ΔAED có

AB=AE

\(\widehat{BAC}=\widehat{EAD}\)(hai góc đối đỉnh)

AC=AD

Do đó: ΔABC=ΔAED
=>BC=ED

2: Xét ΔACD có AC=AD

nên ΔACD cân tại A

Xét ΔABE có AB=AE

nên ΔABE cân tại A

3: ta có: ΔABE cân tại A

mà AM là đường trung tuyến

nên AM\(\perp\)BE

a: Xét ΔABD và ΔAMD có

AB=AM

\(\widehat{BAD}=\widehat{MAD}\)

AD chung

Do đó: ΔABD=ΔAMD

b: Ta có: ΔABD=ΔAMD

=>DB=DM

=>D nằm trên đường trung trực của BM(1)

Ta có: AB=AM

=>A nằm trên đường trung trực của BM(2)

Từ (1) và (2) suy ra AD là đường trung trực của BM

=>AD\(\perp\)BM tại I và I là trung điểm của BM

c: Xét ΔKBA và ΔKPM có

KB=KP

\(\widehat{BKA}=\widehat{PKM}\)(hai góc đối đỉnh)

KA=KM

Do đó: ΔKBA=ΔKPM

=>\(\widehat{KBA}=\widehat{KPM}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//MP

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

b: Xét ΔMAB vuông tại M và ΔMDC vuông tại M có

MB=MC

\(\widehat{MBA}=\widehat{MCD}\)(hai góc so le trong, AB//CD)

Do đó: ΔMAB=ΔMDC

Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

\(\widehat{ABC}=\widehat{DCB}\)(hai góc so le trong, AB//CD)

Do đó: \(\widehat{ACB}=\widehat{DCB}\)

=>CB là phân giác của góc ACD

a: Xét ΔABE và ΔADE có

AB=AD

\(\widehat{BAE}=\widehat{DAE}\)

AE chung

Do đó: ΔABE=ΔADE

b: Ta có: ΔABE=ΔADE

=>EB=ED

=>E nằm trên đường trung trực của BD(1)

Ta có: AB=AD

=>A nằm trên đường trung trực của BD(2)

Từ (1) và (2) suy ra AE là đường trung trực của BD

=>AE\(\perp\)BD tại H và H là trung điểm của BD

c: Xét ΔEBM và ΔEDC có

EB=ED

\(\widehat{BEM}=\widehat{DEC}\)(hai góc đối đỉnh)

EM=EC

Do đó: ΔEBM=ΔEDC

=>\(\widehat{EBM}=\widehat{EDC}\) và BM=DC

Ta có: \(\widehat{EBM}=\widehat{EDC}\)

\(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)

\(\widehat{ABE}=\widehat{ADE}\)(ΔABE=ΔADE)

Do đó: \(\widehat{EBM}+\widehat{EBA}=180^0\)

=>A,B,M thẳng hàng

Ta có: AB+BM=AM

AD+DC=AC

mà AB=AD và BM=DC

nên AM=AC

=>A nằm trên đường trung trực của MC(1)

Ta có: EM=EC

=>E nằm trên đường trung trực của MC(2)

Từ (1) và (2) suy ra AE là đường trung trực của MC

=>AE\(\perp\)MC

mà AE\(\perp\)BD

nên BD//MC

a) Xét △MIQ và △NIP ta có:

            IM=IN (gt)

       ∠MIQ=∠NIP(2 góc đối đỉnh)

          MQ=MP (gt)

Vậy : △MIQ = △NIP (c.g.c)

Vậy: QM = NP (2 cạnh tương ứng)

⇒ ∠MQI = ∠IPN (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong

Vậy : QM // NP

b) Xét △MEK và △PEN ta có:

            EM = EP (gt)

       ∠MEK =∠PEN (2 góc đối đỉnh)

            EK = EN (gt)

⇒ △MEK = △PEN (c.g.c)

⇒ ∠EMK = ∠EPN (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong

Vậy: MK//PN

c) Từ câu a và câu b, ta có : QM//NP và MK//PN

Vậy M,Q,K thẳng hàng.(1)

Ta có:△MEK=△PEN (theo câu b)

⇒ MK=NP (2 cạnh tương ứng)

⇒ QM=NP (theo câu a) và MK=NP(chứng minh trên)⇒QM=MK (2)

Từ (1) và (2), suy ra: M là trung điểm của đoạn thẳng QK.