Mng giúp e bài này vs:
Cho tam giác ABC có AC > AB, M là trung điểm của cạnh BC . Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Nối C với D.
a) Chứng minh góc ADC lớn hơn góc DAC. Từ đó suy ra: góc MAB lớn hơn góc MAC.
b) Kẻ đường cao AH. Gọi E là một điểm nằm giữa A và H. So sánh HC và HB, EC và EB
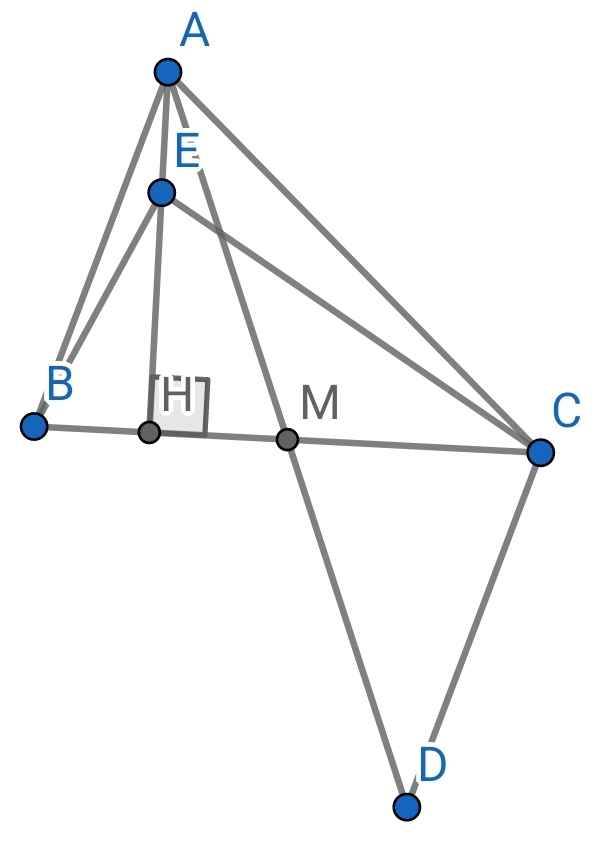
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ AB = CD
Mà AC > AB (gt)
⇒ AC > CD
∆ACD có:
AC > CD (cmt)
⇒ ∠ADC > ∠DAC
Do ∆AMB = ∆DMC (cmt)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
⇒ ∠MAB = ∠ADC
Mà ∠ADC > ∠DAC (cmt)
⇒ ∠MAB > ∠MAC
b) Do AC > AB (gt)
AH là đường vuông góc hạ từ A đến BC
⇒ HC > HB (đường xiên nào lớn hơn thì hình chiếu lớn hơn)
Do E nằm giữa A và H (gt)
⇒ EH là đường vuông góc hạ từ E đến BC
Mà HC > HB (cmt)
⇒ EC > EB (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)

