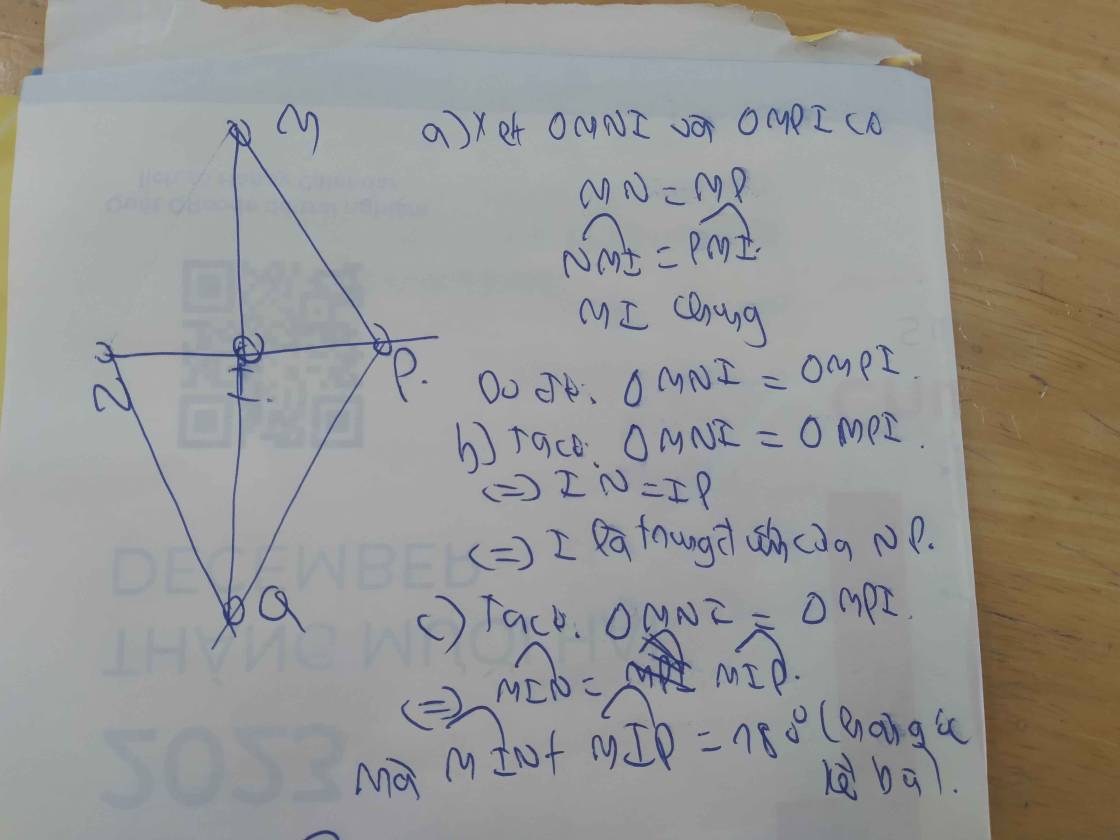
Tam giác MNP có MN = MP. Tia phân giác của góc NMP cắt NP tại I a) Cm ∆MNI = ∆MPI b) Cm I là trung điểm của NP c) Cm MI vuông góc với NP d) Trên tia đối của tia IM lấy điểm Q sao cho IQ = IM. Cm NQ // MP
Chương II : Tam giác
CHO tam giác ABC cân tại A . BH vuông góc AC ( H thuộc AC) .CK vuông góc AB ( K thuộc AB ) .CMR:a) AH=AK. b) KH//BC . c) CK cắt BH tại O . Cmr tam giác OBC cân .
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔABC có \(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
nên KH//BC
c: Ta có: ΔABH=ΔACK
=>\(\widehat{ABH}=\widehat{ACK}\)
Ta có: \(\widehat{OBC}+\widehat{ACB}=90^0\)(ΔHBC vuông tại H)
\(\widehat{OCB}+\widehat{ABC}=90^0\)(ΔKBC vuông tại K)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
Đúng 1
Bình luận (0)
Câu 6. (0,75 điểm) Nhà của bạn An, bạn Bình, bạn Châu lần lượt ở vị trí A, B, và C. Khoảng cách giữa nhà bạn An và nhà bạn Bình là 8,5 km, khoảng cách giữa nhà bạn Bình và nhà bạn Châu là 10 km, khoảng cách giữa nhà bạn An và nhà bạn Châu là 11,5 km và được minh họa (theo Hình 5). Vào dịp cuối tuần, cả ba bạn chọn một vị trí giữa nhà bạn Bình và bạn Châu (vị trí D) để gặp nhau. Chứng minh rằng: Khoảng cách từ nhà bạn An đến chỗ các bạn quyết định gặp nhau luôn có giá trị lớn hơn 5 km và nhỏ hơn...
Đọc tiếp
Câu 6. (0,75 điểm) Nhà của bạn An, bạn Bình, bạn Châu lần lượt ở vị trí A, B, và C. Khoảng cách giữa nhà bạn An và nhà bạn Bình là 8,5 km, khoảng cách giữa nhà bạn Bình và nhà bạn Châu là 10 km, khoảng cách giữa nhà bạn An và nhà bạn Châu là 11,5 km và được minh họa (theo Hình 5). Vào dịp cuối tuần, cả ba bạn chọn một vị trí giữa nhà bạn Bình và bạn Châu (vị trí D) để gặp nhau. Chứng minh rằng: Khoảng cách từ nhà bạn An đến chỗ các bạn quyết định gặp nhau luôn có giá trị lớn hơn 5 km và nhỏ hơn 15 km. Hình ảnh: https://i.imgur.com/Dt12ZPE.jpg
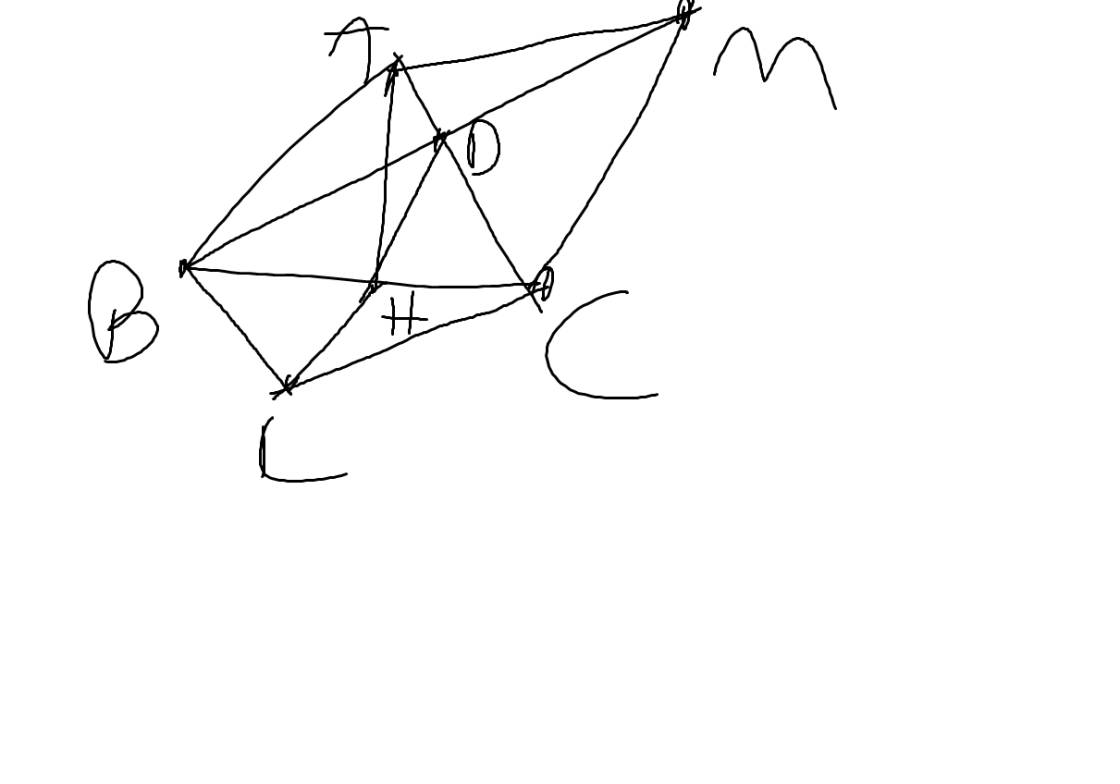
3. (3,0 điểm) Cho tam giác ABC có AB = AC , góc A nhọn. Gọi H là trung điểm của BC. a. Chứng minh tam giác ABH = Tam giác ACH và AH vuông góc với BC. b) Kẻ BD vuông góc AC (D thuộc AC) . Trên tia DH, lấy K sao cho H là trung điểm của DK. Cm: Tam giác HDB = Tam giác HKC c) Trên tia đối của tia DB lấy điểm M sao cho DM = DB .Chứng minh DMC = 1/2BAC Vẽ hình (không cần lời giải)
3. (3,0 điểm) Cho tam giác ABC có AB = AC , góc A nhọn. Gọi H là trung điểm của BC. a. Chứng minh tam giác ABH = Tam giác ACH và AH vuông góc với BC. b) Kẻ BD vuông góc AC (D thuộc AC) . Trên tia DH, lấy K sao cho H là trung điểm của DK. Cm: Tam giác HDB = Tam giác HKC c) Trên tia đối của tia DB lấy điểm M sao cho DM = DB .Chứng minh DMC = 1/2BAC
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC tại H
b: Xét ΔHDB và ΔHKC có
HD=HK
\(\widehat{DHB}=\widehat{KHC}\)(hai góc đối đỉnh)
HB=HC
Do đó: ΔHDB=ΔHKC
c: Ta có: DM=DB
mà D nằm giữa M và B
nên D là trung điểm của BM
Xét ΔCBM có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔCBM cân tại C
=>\(\widehat{CBM}=\widehat{CMB}\)
mà \(\widehat{CBM}=\widehat{HAC}\left(=90^0-\widehat{ACH}\right)\)
nên \(\widehat{CMB}=\widehat{HAC}\left(1\right)\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{1}{2}\cdot\widehat{BAC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{DMC}=\dfrac{1}{2}\cdot\widehat{BAC}\)
Đúng 1
Bình luận (2)
Cho tam giác ABC cân tại A . Tia phân giác của góc A cắt BC tại H . Kẻ HK vuông góc với AB, HM vuông góc với AC. Chứng minh: A) tam giác HAK = tam giác HAM B) tam giác KAM cân và KM song song BC C) lấy E thuộc AH. Trên tia đối của EM lấy I sao cho E là trung điểm của IM. Chứng minh KI song song AH Giúp mình giải và vẽ hình với ạ cảm ơn ạ!!
a: Xét ΔHAK vuông tại K và ΔHAM vuông tại M có
AH chung
\(\widehat{HAK}=\widehat{HAM}\)(AH là phân giác của góc KAM)
Do đó: ΔHAK=ΔHAM
b: Ta có: ΔHAK=ΔHAM
=>AK=AM
=>ΔAKM cân tại A
Xét ΔABC có \(\dfrac{AK}{AB}=\dfrac{AM}{AC}\)
nên KM//BC
Đúng 3
Bình luận (0)
Bài 9. Cho tam giác ABC vuông tại A và AB AC . Qua A kẻ đường thẳng d cắt BC . VẽBM ,CN vuông góc với d . Chứng minh rằng : DBAM DACN . ai giup mk voi
Đọc tiếp
Bài 9. Cho tam giác ABC vuông tại A và AB = AC . Qua A kẻ đường thẳng d cắt BC . Vẽ
BM ,CN vuông góc với d . Chứng minh rằng : DBAM = DACN .
ai giup mk voi
Ta có: \(\widehat{BAM}+\widehat{BAC}+\widehat{CAN}=180^0\)
=>\(\widehat{BAM}+\widehat{CAN}+90^0=180^0\)
=>\(\widehat{BAM}+\widehat{CAN}=90^0\)
mà \(\widehat{BAM}+\widehat{MBA}=90^0\)(ΔMAB vuông tại M)
nên \(\widehat{CAN}=\widehat{MBA}\)
Xét ΔMBA vuông tại M và ΔNAC vuông tại N có
BA=AC
\(\widehat{MBA}=\widehat{NAC}\)
Do đó: ΔMBA=ΔNAC
Đúng 0
Bình luận (0)
ai giup mk dc ko B D C
Đọc tiếp
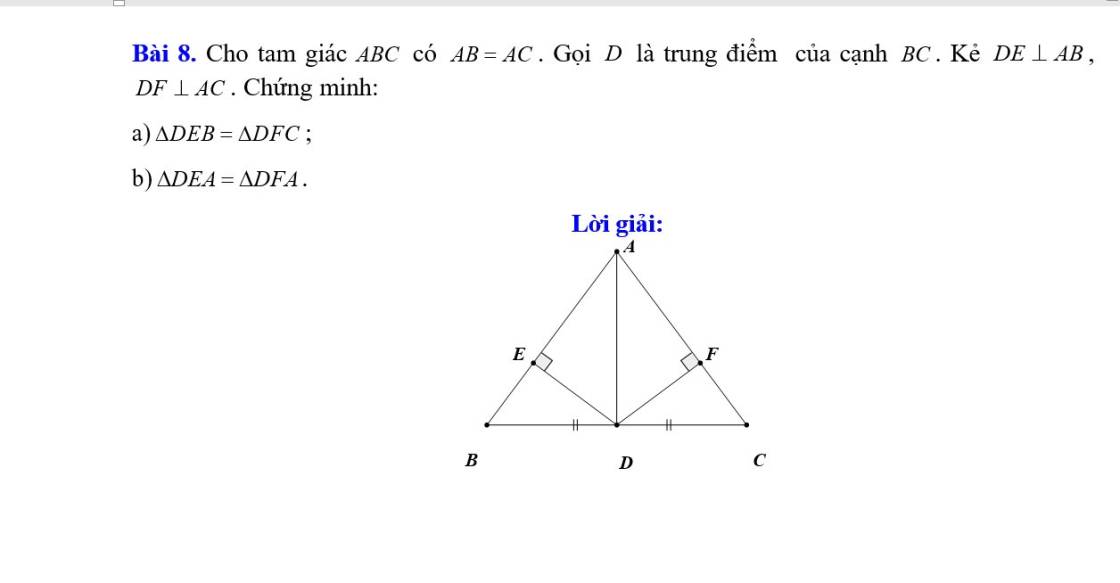
ai giup mk dc ko
B D C
`a)`
Vì `AB=AC`
`=>△ABC` cân tại `A`
Mà `AD` là đường trung tuyến
`=>AD` là đường trung trực, đường phân giác, đường trung tuyến của `△ABC`
`=>hat(DAB)=hat(DAC)`
Xét `△DEB` và `△DFC` có `:`
`DB=DC(` gt `)`
`hat(BED)=hat(CFD)=90^o`
`hat(B)=hat(C)(△ABC` cân tại `A)`
`=>△DEB=△DFC(` cạnh huyền - góc nhọn `)`
`b)`
Xét `△DEA` và `△DFA` có `:`
Chung `AD`
`hat(AED)=hat(AFD)=90^o`
`hat(DAB)=hat(DAC)` (cmt)
`=>△DEA=△DFA(` cạnh huyền - góc nhọn` )`
Đúng 1
Bình luận (0)
cho tam giác abc, gọi m là trung điểm của a. trên tia đối của tia mc, lấy e sao cho me =mc
a) chứng minh tam giác mae = tam giác mbc
b) chứng minh ea song song bc
c) trên tia ca lấy điểm f sao cho fa = ca. chứng minh góc fea = góc abc
d) trên tia cb lấy điểm d sao cho db = cb. chứng minh d, e, f thẳng hàng
a: Sửa đề: M là trung điểm của AB
Xét ΔMAE và ΔMBC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)
ME=MC
Do đó: ΔMAE=ΔMBC
b: ta có: ΔMAE=ΔMBC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
c: Ta có: FA=CA
mà A nằm giữa Fvà C
nên A là trung điểm của CF
Xét ΔCFE có
A,M lần lượt là trung điểm của CF,CE
=>AM là đường trung bình của ΔCFE
=>AM//FE
=>\(\widehat{BAE}=\widehat{FEA}\)
mà \(\widehat{BAE}=\widehat{CBA}\)
nên \(\widehat{CBA}=\widehat{FEA}\)
d: Xét ΔCED có
M,B lần lượt là trung điểm của CE,CD
=>MB là đường trung bình của ΔCED
=>MB//ED
=>AB//ED
Ta có: AM//FE
M\(\in\)AB
Do đó: AB//FE
mà AB//ED
mà FE,ED có điểm chung là E
nên F,E,D thẳng hàng
Đúng 2
Bình luận (1)
cho t/g ABC vuông tại A. Vẽ AH vuông tại B (H thuộc BC). Trên BC và BA lấy M và N sao cho AN=AH,CM=CA.CMR
a) MN vuông tại AB
b) BC + AH > AC + AB
a: Xét ΔCAM có CA=CM
nên ΔCAM cân tại C
=>\(\widehat{CAM}=\widehat{CMA}\)
Ta có: \(\widehat{CAM}+\widehat{BAM}=\widehat{BAC}=90^0\)
\(\widehat{CMA}+\widehat{HAM}=90^0\)(ΔHAM vuông tại H)
mà \(\widehat{CAM}=\widehat{CMA}\)
nên \(\widehat{BAM}=\widehat{HAM}\)
Xét ΔAHM và ΔANM có
AH=AN
\(\widehat{HAM}=\widehat{NAM}\)
AM chung
Do đó: ΔAHM=ΔANM
=>\(\widehat{AHM}=\widehat{ANM}\)
mà \(\widehat{AHM}=90^0\)
nên \(\widehat{ANM}=90^0\)
=>MN\(\perp\)AB
b:
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
\(\left(BC+AH\right)^2=BC^2+2\cdot BC\cdot AH+AH^2\)
\(=AB^2+AC^2+2\cdot AB\cdot AC+AH^2\)
\(=\left(AB+AC\right)^2+AH^2\)
=>\(\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
=>BC+AH>AB+AC
Đúng 1
Bình luận (0)