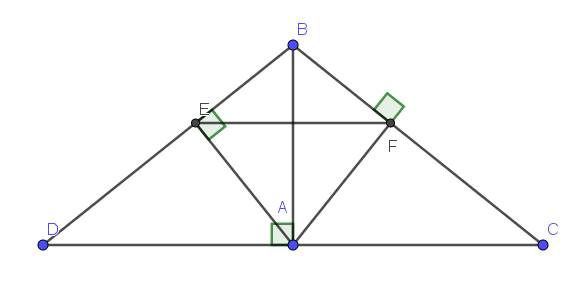
a: Xét ΔBAC vuông tại A và ΔBAD vuông tại A có
BA chung
AC=AD
Do đó;ΔBAC=ΔBAD
b: Ta có: ΔBAC=ΔBAD
=>\(\widehat{ABC}=\widehat{ABD}\)
Xét ΔBEA vuông tại E và ΔBFA vuông tại F có
BA chung
\(\widehat{EBA}=\widehat{FBA}\)
Do đó: ΔBEA=ΔBFA
=>AE=AF
=>ΔAEF cân tại A
c: ta có: ΔBEA=ΔBFA
=>BE=BF
Xét ΔBDC có \(\dfrac{BE}{BD}=\dfrac{BF}{BC}\)
nên EF//DC
Lời giải:
a.
Tam giác $ABC$ vuông tại $A\Rightarrow \widehat{BAC}=90^0$
$\widehat{BAD}=180^0-\widehat{BAC}=180^0-90^0=90^0$
Xét tam giác $ABC$ và $ABD$ có:
$AB$ chung
$\widehat{BAC}=\widehat{BAD}=90^0$
$AD=AC$ (gt)
$\Rightarrow \triangle ABC=\triangle ABD$ (c.g.c)
b.
Từ tam giác bằng nhau phần a
$\Rightarrow \widehat{DBA}=\widehat{CBA}$
$\Rightarrow \widehat{EBA}=\widehat{FBA}$
Xét tam giác $EBA$ và $FBA$ có:
$\widehat{EBA}=\widehat{FBA}$ (cmt)
$\widehat{BEA}=\widehat{BFA}=90^0$
$BA$ chung
$\Rightarrow \triangle EBA=\triangle FBA$ (ch-gn)
$\Rightarrow EA=FA$
$\Rightarrow AEF$ cân tại $A$.
c.
Từ tam giác bằng nhau phần b
$\Rightarrow BE=BF, AE=AF$
$\Rightarrow BA$ là trung trực của $EF$
$\Rightarrow BA\perp EF$
Mà $BA\perp DC$
$\Rightarrow EF\parallel DC$