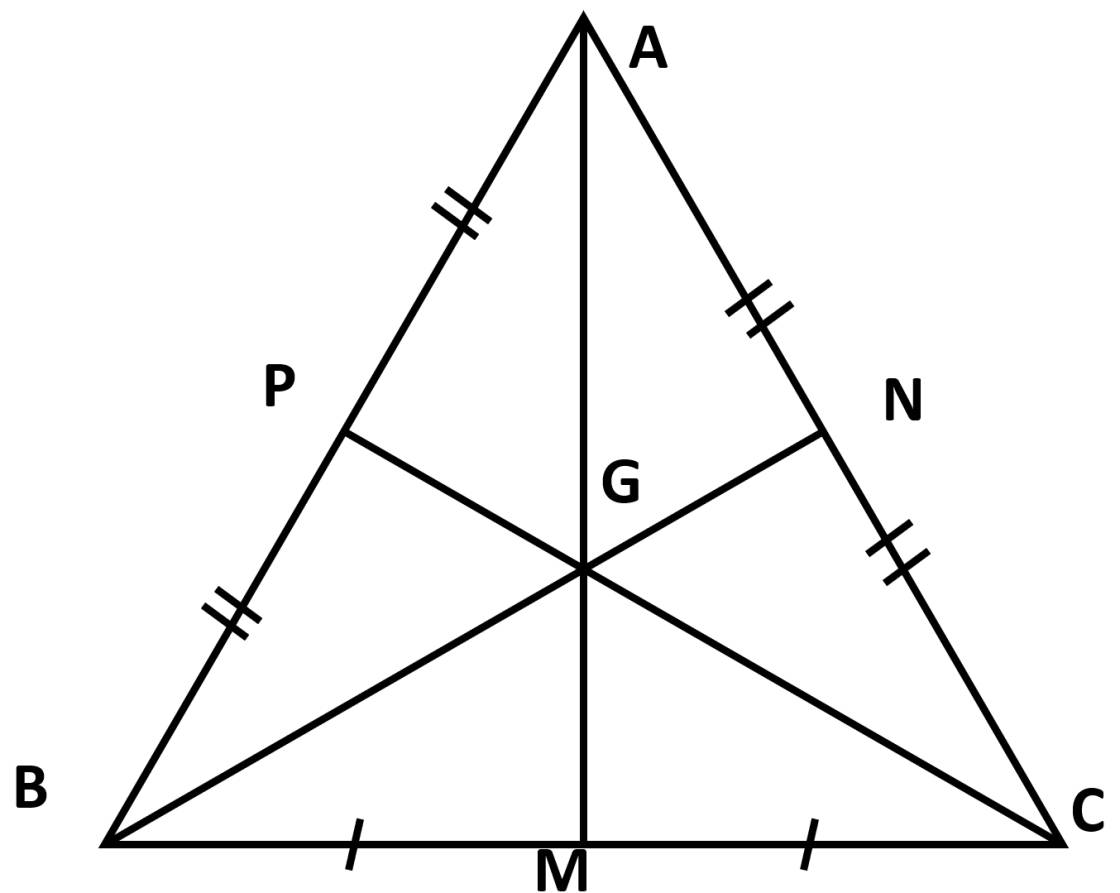
a) vì G là trọng tâm của \(\Delta ABC\) nên ta có:
\(AG=\dfrac{2}{3}\cdot AM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
b) ta có AM là đường trung tuyến của ΔABC
lại có: ΔABC là Δ cân
⇒ AM cũng là đường cao của ΔABC
⇒ AM ⊥ BC
c) ta có AM là đường trung tuyến của ΔABC
lại có: ΔABC là Δ cân
⇒ AM cũng là đường phân giác của ΔABC
⇒ AM là tia phân giác của \(\widehat{BAC}\)
d) ta có: \(AB=AC\) (vì ΔABC cân tại A)
\(\Rightarrow\dfrac{1}{2}\cdot AB=\dfrac{1}{2}\cdot AC=PB=NC\)
Xét △PBC và △NCB, có:
PB = NC (cmt)
\(\widehat{ABC}=\widehat{ACB}\) (Vì △ABC cân tại A)
BC là cạnh chung
⇒ △PBC và △NCB (c-g-c)
⇒ PC = BN (2 cạnh tương ứng)
độ dài cạnh BN là:
\(6:\dfrac{2}{3}=9\left(cm\right)\)
CP = BN = 9 (cm)
vậy cạnh CP = 9cm