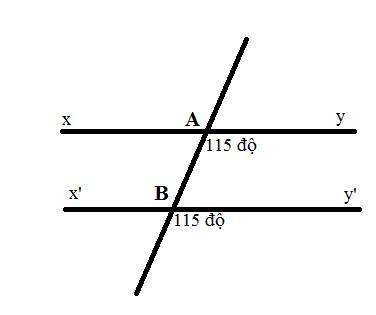
Chứng tỏ xy // x'y'

Chứng tỏ xy // x'y'
Vẽ lại hình:
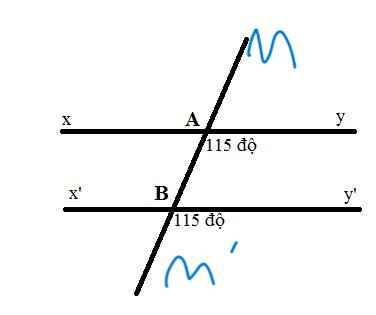
\(\widehat{x'BA}=\widehat{y'Bm'}\)(hai góc đối đỉnh)
=>\(\widehat{x'BA}=115^0\)
\(\widehat{x'BA}=\widehat{yAB}\)
mà hai góc này ở vị trí so le trong
nên xx'//yy'
mn giúp mk câu 3 với 
Ta có:
∠x'AB + ∠x'Az = 180⁰ (kề bù)
⇒ ∠x'AB = 180⁰ - ∠x'Az
= 180⁰ - 120⁰
= 60⁰
⇒ ∠x'AB = ∠y'Bz' = 60⁰
Mà ∠x'AB và ∠y'Bz' là hai góc so le trong
⇒ xx' // yy'
mn giúp mk câu 2 và 4 với 
Cho hình vẽ sau:
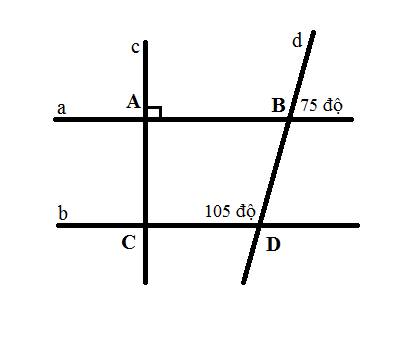
a) Tính số đo góc ABD?
b) Chứng minh a//b
c) Chứng minh \(c\perp b\)
a) Do \(\widehat{ABD}\) đổi đỉnh với góc bên ngoài
\(\Rightarrow\widehat{ABD}=75^o\)
b) Ta có \(\widehat{ABd}=180^o-75^o=105^o\) (kể bù)
\(\Rightarrow\widehat{\text{C}DB}=\widehat{ABd}=105^o\)
Mà hai góc này ở vị trí đồng vị
\(\Rightarrow a//b\)
d) Ta có: \(a//b\) và \(a\perp c\)
\(\Rightarrow b\perp c\)
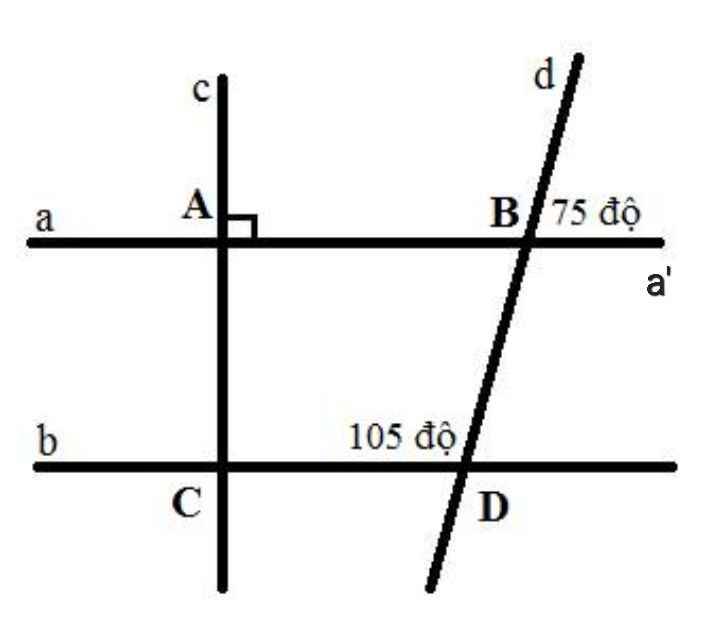 a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
⇒ ∠ABD = ∠dBa' = 75⁰
b) Ta có:
∠ABD + ∠a'BD = 180⁰ (kề bù)
⇒ ∠a'BD = 180⁰ - ∠ABD
= 180⁰ - 75⁰
= 105⁰
⇒ ∠a'BD = ∠CDB = 105⁰
Mà ∠a'BD và ∠CDB là hai góc so le trong
⇒ a // b
c) Do c ⊥ a (gt)
a // b (cmt)
⇒ c ⊥ b
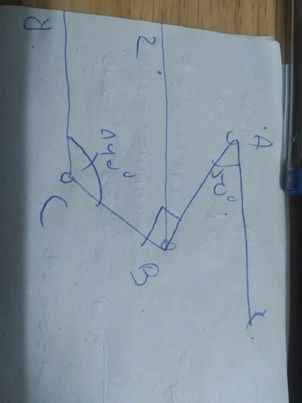
Bài 3:
Kẻ Bz//Ax(Bz và Ax nằm ở hai mặt phẳng bờ đối nhau của đoạn thẳng BA)
Bz//Ax
=>\(\widehat{xAB}=\widehat{zBA}\)(hai góc so le trong)
=>\(\widehat{zBA}=50^0\)
\(\widehat{zBA}+\widehat{zBC}=\widehat{ABC}\)
=>\(\widehat{zBC}+50^0=90^0\)
=>\(\widehat{zBC}=40^0\)
\(\widehat{zBC}+\widehat{yCB}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Bz//Cy
Ax//Bz
Bz//Cy
Do đó: Ax//Cy
Bài 2:
\(\widehat{A_1}=\widehat{A_3}\)(hai góc đối đỉnh)
mà \(\widehat{A_1}=70^0\)
nên \(\widehat{A_3}=70^0\)
\(\widehat{A_1}+\widehat{A_2}=180^0\)(hai góc kề bù)
=>\(\widehat{A_2}+70^0=180^0\)
=>\(\widehat{A_2}=110^0\)
\(\widehat{A_2}=\widehat{A_4}\)(hai góc đối đỉnh)
mà \(\widehat{A_2}=110^0\)
nên \(\widehat{A_4}=110^0\)
\(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)
mà \(\widehat{B_4}=70^0\)
nên \(\widehat{B_2}=70^0\)
\(\widehat{B_4}+\widehat{B_1}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}+70^0=180^0\)
=>\(\widehat{B_1}=110^0\)
\(\widehat{B_1}=\widehat{B_3}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=110^0\)
nên \(\widehat{B_3}=110^0\)
`# \text {DNamNgV}`
`1,`
Ta có:
\(\widehat{\text{mOn}}+\widehat{\text{nOp}}=\widehat{\text{ }\text{mOp}}\\ \Rightarrow30^0+\widehat{\text{nOp}}=70^0\\ \Rightarrow\widehat{\text{nOp}}=40^0\)
Vậy, \(\widehat{\text{nOp}}=40^0.\)
`2,`
*Thiếu chữ z ở tia Oz kìa cậu :'>*
Vì \(\widehat{\text{xOz}}\) và \(\widehat{\text{yOz}}\) là `2` góc kề bù
\(\Rightarrow\widehat{\text{xOz}}+\widehat{\text{yOz}}=180^0\\ \Rightarrow\widehat{\text{xOz}}+135^0=180^0\\ \Rightarrow\widehat{\text{xOz}}=45^0\)
Vậy, \(\widehat{\text{xOz}}=45^0.\)
b1
ta có : góc POM = góc PON + góc MON => 70 = PON + 30 => góc PON = 40 độ
b2
ta thấy đc XOZ kề bù v YOZ => XOZ + YOZ =180 độ
=> XOZ = 45 độ
Có 2 cặp góc đối đỉnh được tạo thành khác góc bẹt:
\(\widehat{xAy}\) và \(\widehat{x'Ay'}\); \(\widehat{xAy'}\) và \(\widehat{x'Ay}\)
cho hai đường thẳng mn và pq cắt nhau tại o.tính các góc tạo thành biết góc mop= 2/3 moq
góc mOp+góc mOq=180 độ
góc mOp=2/3*góc mOq
=>góc mOp=2/5*180=72 độ và góc mOq=180-72=108 độ
góc mOp=góc nOq(đối đỉnh)
mà góc mOp=72 độ
nên góc nOq=72 độ
góc mOq=góc nOp(đối đỉnh)
mà góc mOq=108 độ
nên góc nOp=108 độ
mik cần gấp , kèm hình .
a)
Ta có : AC = BD (GT)
Mà OA = OB (GT)
=> OC = OD
Xét \(\Delta AOD\) = \(\Delta BOC\) có :
OA = OB (GT)
OC = OD (C/M trên)
\(\widehat{AOD}\) = \(\widehat{BOC}\) ( 2 góc đối đỉnh )
=> \(\Delta AOD\) = \(\Delta BOC\) (c.g.c)
=> AD = BC ( 2 cạnh tương ứng )
b)
Vì \(\Delta AOD\) = \(\Delta BOC\) (câu a)
\(\widehat{CBO}\) = \(\widehat{DAO}\) ( 2 góc tương ứng )
Ta có :
\(\widehat{CBO}\) + \(\widehat{OBE}\) = \(180^o\) ( 2 góc kề bù )
\(\widehat{DAO}\) + \(\widehat{OAE}\) = \(180^o\) ( 2 góc kề bù )
Mà \(\widehat{CBO}\) = \(\widehat{DAO}\)
=> \(\widehat{EAC}\) = \(\widehat{EBD}\) (ĐPCM)
c)
cho xOy và yOx là 2 góc kề bù biết xOy - yOz = 50 độ . Tính góc xOy và yOz
cần gấp ạ
Góc xOy và yOz là hai góc kề bù nên xOy + yOz = 180°
xOy - yOz = 50°
xOy + yOz - (xOy - yOz) = 180° - 50°
2yOz = 130°
yOz = 65°
xOy = 180° - yOz = 180° - 65° = 115°
Vậy góc xOy = 115° và yOz = 65°