Question

Answer 1

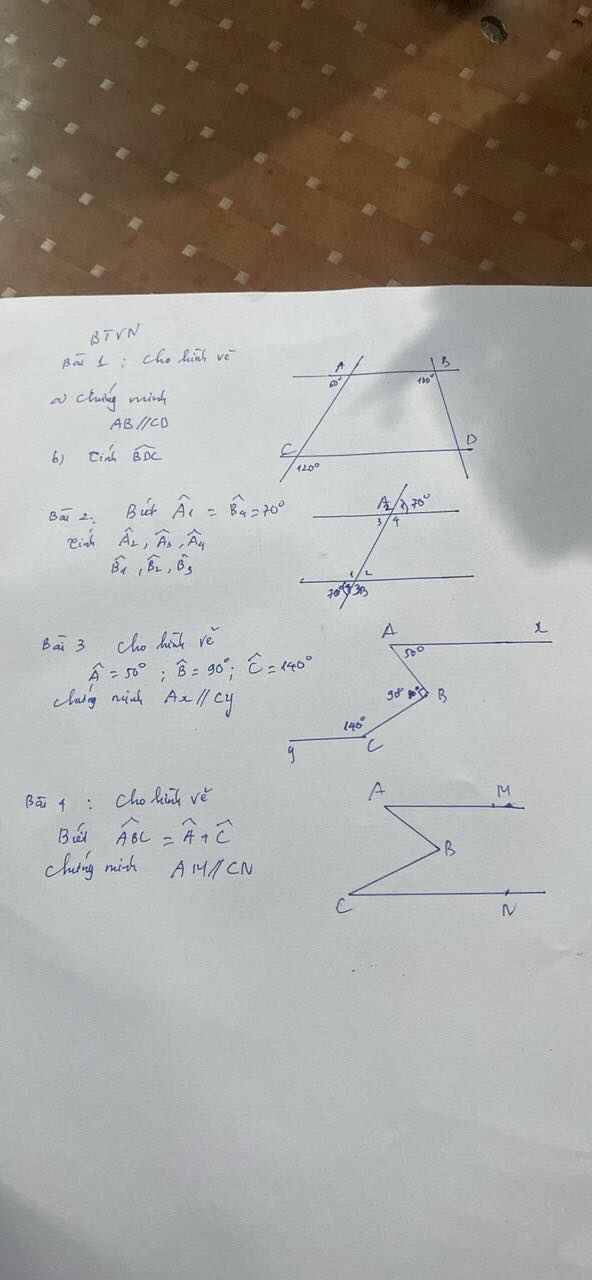
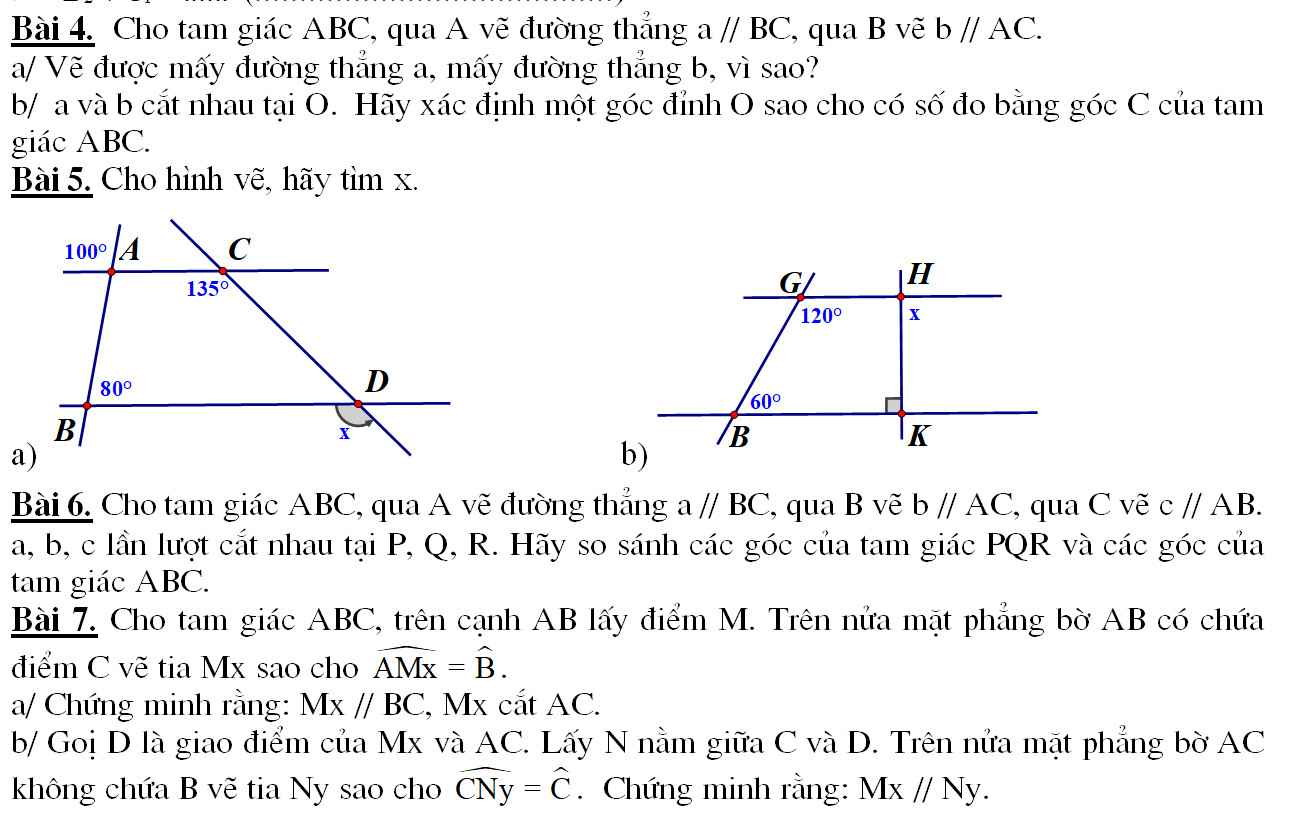
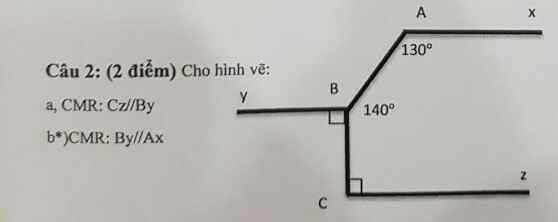
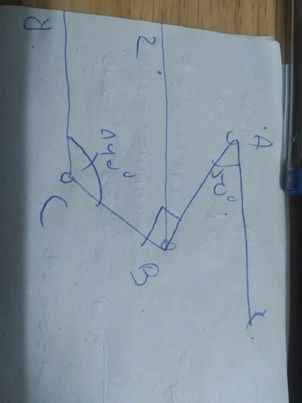
Bài 3:

Kẻ Bz//Ax(Bz và Ax nằm ở hai mặt phẳng bờ đối nhau của đoạn thẳng BA)

Bz//Ax

=>\(\widehat{xAB}=\widehat{zBA}\)(hai góc so le trong)

=>\(\widehat{zBA}=50^0\)

\(\widehat{zBA}+\widehat{zBC}=\widehat{ABC}\)

=>\(\widehat{zBC}+50^0=90^0\)

=>\(\widehat{zBC}=40^0\)

\(\widehat{zBC}+\widehat{yCB}=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên Bz//Cy

Ax//Bz

Bz//Cy

Do đó: Ax//Cy

Bài 2:

\(\widehat{A_1}=\widehat{A_3}\)(hai góc đối đỉnh)

mà \(\widehat{A_1}=70^0\)

nên \(\widehat{A_3}=70^0\)

\(\widehat{A_1}+\widehat{A_2}=180^0\)(hai góc kề bù)

=>\(\widehat{A_2}+70^0=180^0\)

=>\(\widehat{A_2}=110^0\)

\(\widehat{A_2}=\widehat{A_4}\)(hai góc đối đỉnh)

mà \(\widehat{A_2}=110^0\)

nên \(\widehat{A_4}=110^0\)

\(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)

mà \(\widehat{B_4}=70^0\)

nên \(\widehat{B_2}=70^0\)

\(\widehat{B_4}+\widehat{B_1}=180^0\)(hai góc kề bù)

=>\(\widehat{B_1}+70^0=180^0\)

=>\(\widehat{B_1}=110^0\)

\(\widehat{B_1}=\widehat{B_3}\)(hai góc đối đỉnh)

mà \(\widehat{B_1}=110^0\)

nên \(\widehat{B_3}=110^0\)