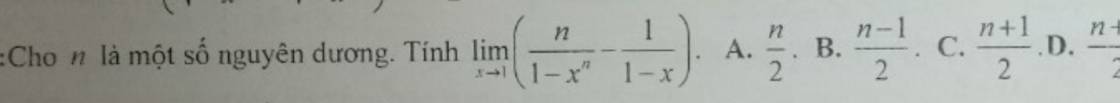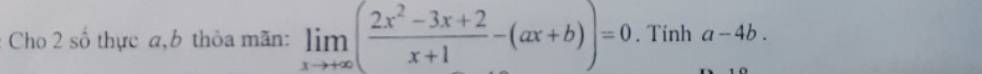Chương 4: GIỚI HẠN

Dạng \(u_{n+1}=\dfrac{au_n+b}{cu_n+d}\) này có 1 cách làm chung:

Đặt \(v_n=u_n+k\) với k sao cho sau khi chuyển vế rút gọn thì tử số của \(\dfrac{au_n+b}{cu_n+d}\) triệt tiêu mất số hạng tự do b là được.

Ví dụ ở bài này, ta đặt ra nháp:

\(u_n=v_n+k\Rightarrow v_{n+1}+k=\dfrac{4\left(v_n+k\right)+2}{v_n+3+k}\)

\(\Rightarrow v_{n+1}=\dfrac{4v_n+4k+2}{v_n+k+3}-k=\dfrac{4v_n+4k+2-k\left(v_n+k+3\right)}{v_n+k+3}\)

\(=\dfrac{\left(4-k\right)v_n+2-k^2+k}{v_n+k+3}\)

Cần k sao cho \(-k^2+k+2=0\Rightarrow k=-1\) (lấy số nhỏ cho gọn). Vậy là xong. Thực tế ta làm như sau:

Đặt \(u_n=v_n-1\Rightarrow v_1=u_1+1=4\)

\(v_{n+1}-1=\dfrac{4\left(v_n-1\right)+2}{v_n+2}\Rightarrow v_{n+1}=\dfrac{4v_n-2}{v_n+2}+1=\dfrac{5v_n}{v_n+2}\)

(sau đó nghịch đảo 2 vế):

\(\Rightarrow\dfrac{1}{v_{n+1}}=\dfrac{v_n+2}{5v_n}=\dfrac{2}{5}.\dfrac{1}{v_n}+\dfrac{1}{5}\)

(Đây là gần như 1 dãy bình thường rồi)

(Tiếp tục đặt \(\dfrac{1}{v_n}=x_n+k\) sao cho triệt tiêu nốt số hạng \(\dfrac{1}{5}\) bên phải đi:

\(x_{n+1}+k=\dfrac{2}{5}\left(x_n+k\right)+\dfrac{1}{5}\Rightarrow x_{n+1}=\dfrac{2}{5}.x_n+\dfrac{2k}{5}+\dfrac{1}{5}-k\)

\(\Rightarrow\dfrac{2k}{5}+\dfrac{1}{5}-k=0\Rightarrow k=\dfrac{1}{3}\))

Đặt \(\dfrac{1}{v_n}=x_n+\dfrac{1}{3}\Rightarrow x_1=\dfrac{1}{v_1}-\dfrac{1}{3}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)

\(\Rightarrow x_{n+1}+\dfrac{1}{3}=\dfrac{2}{5}\left(x_n+\dfrac{1}{3}\right)+\dfrac{1}{5}\Leftrightarrow x_{n+1}=\dfrac{2}{5}x_n\)

Đây là công thức cấp số nhân dạng , do đó ta có: \(x_n=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}\)

\(\Rightarrow\dfrac{1}{v_n}=x_n+\dfrac{1}{3}=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}+\dfrac{1}{3}=-\dfrac{2^{n-1}}{12.5^{n-1}}+\dfrac{4.5^{n-1}}{12}=\dfrac{4.5^{n-1}-2^{n-1}}{12.5^{n-1}}\)

\(\Rightarrow v_n=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}\)

\(\Rightarrow u_n=v_n-1=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}-1\)

\(lim\left(u_n+4\right)=lim\left(\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}+3\right)=\dfrac{12}{4}+3=6\)

Đây là cách làm cơ bản, còn trên thực tế, khi trắc nghiệm chỉ cần đơn giản như sau:

Giả sử \(lim\left(u_n\right)=a\), hiển nhiên dãy đã cho dương nên a dương

Lấy giới hạn 2 vế giả thiết:

\(lim\left(u_{n+1}\right)=lim\left(\dfrac{4u_n+2}{u_n+3}\right)\Rightarrow a=\dfrac{4a+2}{a+3}\)

\(\Rightarrow a^2+3a=4a+2\)

\(\Rightarrow a^2-a-2=0\Rightarrow\left[{}\begin{matrix}a=-1\\a=2\end{matrix}\right.\) \(\Rightarrow a=2\)

\(\Rightarrow lim\left(u_n+4\right)=2+4=6\)

Nhanh hơn khoảng 1 tỉ lần :D

\(\left(1-n\right)\left(\dfrac{-6n}{\sqrt[2]{n^2-6n}+n}+\dfrac{27n^2}{n^2+n\sqrt[3]{n^3-27n^2}+\sqrt[3]{\left(n^3-27n^2\right)^2}}\right)\)

Ngoặc sau giới hạn hữu hạn tới \(\dfrac{27}{3}-\dfrac{6}{2}=6>0\), ngoặc trước tới âm vô cùng, nên giới hạn bằng âm vô cùng

\(\lim\limits_{x\rightarrow1}\dfrac{n\left(1-x\right)-\left(1-x^n\right)}{\left(1-x\right)\left(1-x^n\right)}=\lim\limits_{x\rightarrow1}\dfrac{n-1-nx+x^n}{1-x^n-x+x^{n+1}}\)

L'Hopital:

\(=\lim\limits_{x\rightarrow1}\dfrac{-n+n.x^{n-1}}{-n.x^{n-1}-1+\left(n+1\right)x^n}=\lim\limits_{x\rightarrow1}\dfrac{n\left(n-1\right)x^{n-2}}{-n\left(n-1\right).x^{n-2}+n\left(n+1\right)x^{n-1}}\)

\(=\dfrac{n\left(n-1\right)}{n\left(n+1\right)-n\left(n-1\right)}=\dfrac{n-1}{2}\)

\(\sqrt{a+12}-\sqrt[3]{81+63-19}=0\Rightarrow a=13\)

Khi đó

\(\dfrac{\sqrt{13x^2+4x+8}-\sqrt[3]{81x^2+63x-19}}{\left(x-1\right)^2\left(x+1\right)}\)

\(=\dfrac{\sqrt[]{13x^2+4x+8}-\left(3x+2\right)+\left(3x+2-\sqrt[3]{81x^2+83x-19}\right)}{\left(x-1\right)^2\left(x+1\right)}\)

\(=\dfrac{\dfrac{4\left(x-1\right)^2}{\sqrt[]{13x^2+4x+8}+\left(3x+2\right)}+\dfrac{27\left(x-1\right)^2\left(x+1\right)}{\left(3x+2\right)^2+\left(3x+2\right)\sqrt[3]{81x^2+63x-19}+\sqrt[3]{\left(81x^2+63x-19\right)^2}}}{\left(x-1\right)^2\left(x+1\right)}\)

Giới hạn đã cho hữu hạn nên \(a=-1\)

\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(b-x\right)^2-\left(x^2-6x+2\right)}{b-x+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(6-2b\right)x+b^2-2}{-x+\sqrt{x^2-6x+2}+b}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{6-2b+\dfrac{b^2-2}{x}}{-1-\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}+\dfrac{b}{x}}=\dfrac{6-2b}{-2}=5\)

\(\Rightarrow b=8\)

Cả 4 đáp án đều sai, số lớn hơn là 8

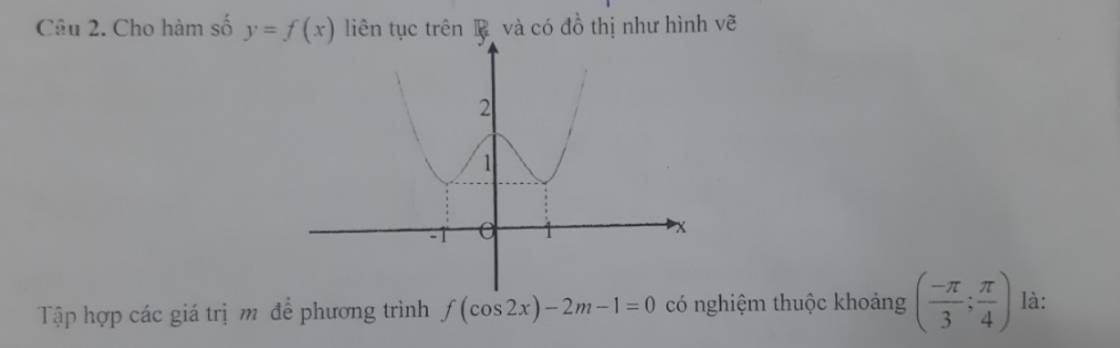
Khi \(-\dfrac{\pi}{3}< x< \dfrac{\pi}{4}\Rightarrow-\dfrac{1}{2}< cos2x< 1\) (đường tròn lượng giác)

Nhìn đồ thị trên \(\left(-\dfrac{1}{2};1\right)\) \(\Rightarrow1< 2m+1< 2\)

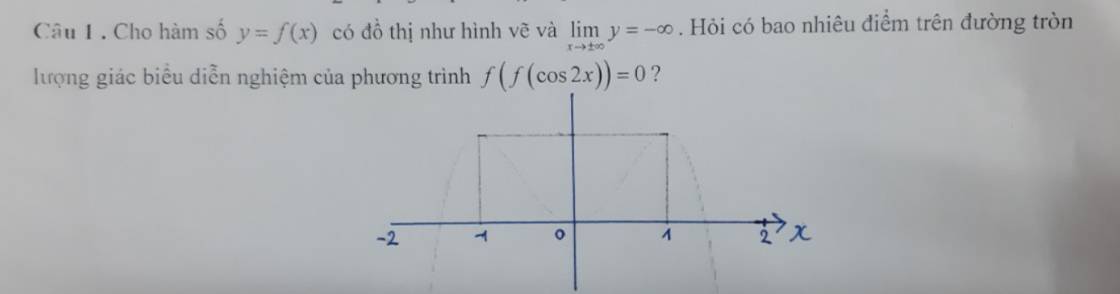
Tìm miền giá trị từ trong ra ngoài sau đó phân tích ngược từ ngoài vào trong:

\(-1\le cos2x\le1\Rightarrow0\le f\left(cos2x\right)\le1\)

Để dễ hình dung, ta đặt \(f\left(cos2x\right)=t\in\left[0;1\right]\)

Trên đoạn này, \(f\left(t\right)=0\) có đúng 1 nghiệm \(t=0\)

\(\Rightarrow f\left(cos2x\right)=0\)

Trên \(\left[-1;1\right]\) pt \(f\left(x\right)=0\) cũng có đúng 1 nghiệm \(x=0\)

\(\Rightarrow cos2x=0\)

Pt này có 4 điểm biểu diễn

bài này hình như đã làm rồi thì phải?

\(\dfrac{2x^2-3x+2-\left(x+1\right)\left(ax+b\right)}{x+1}=\dfrac{\left(2-a\right)x^2-\left(a+b+3\right)x+2-b}{x+1}\)

Đến đoạn này thì nhớ ra là em hỏi rồi thật

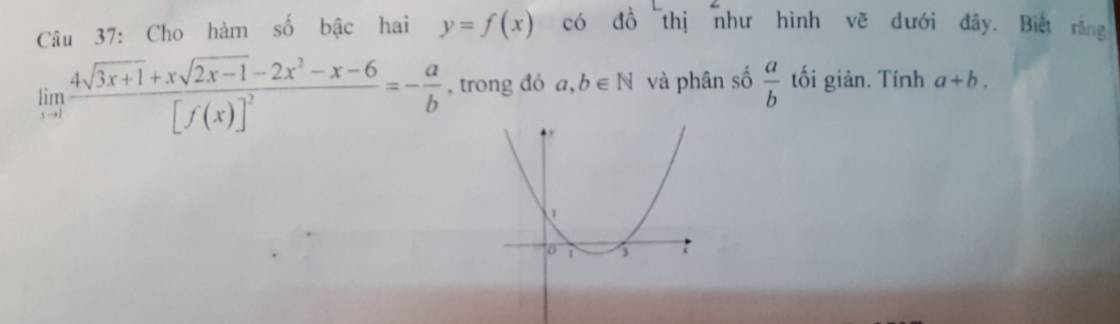
Từ đồ thị \(\Rightarrow f\left(1\right)=f\left(3\right)=0\)

Mà \(f\left(x\right)\) bậc 2 nên \(f\left(x\right)=k\left(x-1\right)\left(x-3\right)\) với k là số thực nào đó

Đồ thị \(f\left(x\right)\) qua \(\left(0;1\right)\Rightarrow3k=1\Rightarrow k=\dfrac{1}{3}\)

\(\Rightarrow f\left(x\right)=\dfrac{1}{3}\left(x-1\right)\left(x-3\right)\)

Thế vào:

\(\dfrac{4\sqrt{3x+1}+x\sqrt{2x-1}-2x^2-x-6}{\dfrac{1}{9}\left(x-1\right)^2\left(x-3\right)^2}\)

\(=\dfrac{-x\left(x-\sqrt{2x-1}\right)-\left(3x+5-4\sqrt{3x+1}\right)-\left(x-1\right)^2}{\dfrac{1}{9}\left(x-1\right)^2\left(x-3\right)^2}\)

Liên hợp 2 ngoặc đầu sẽ khử được hết

Bài này cần nghịch suy ra hàm cụ thể trước khi làm giới hạn

\(=\lim\limits_{x\rightarrow-\infty}\sqrt[3]{\dfrac{\dfrac{2}{x}-1}{8-\dfrac{1}{x}+\dfrac{3}{x^2}}}=\sqrt[3]{\dfrac{-1}{8}}=-\dfrac{1}{2}\)