Bài 7: Ôn tập cuối năm

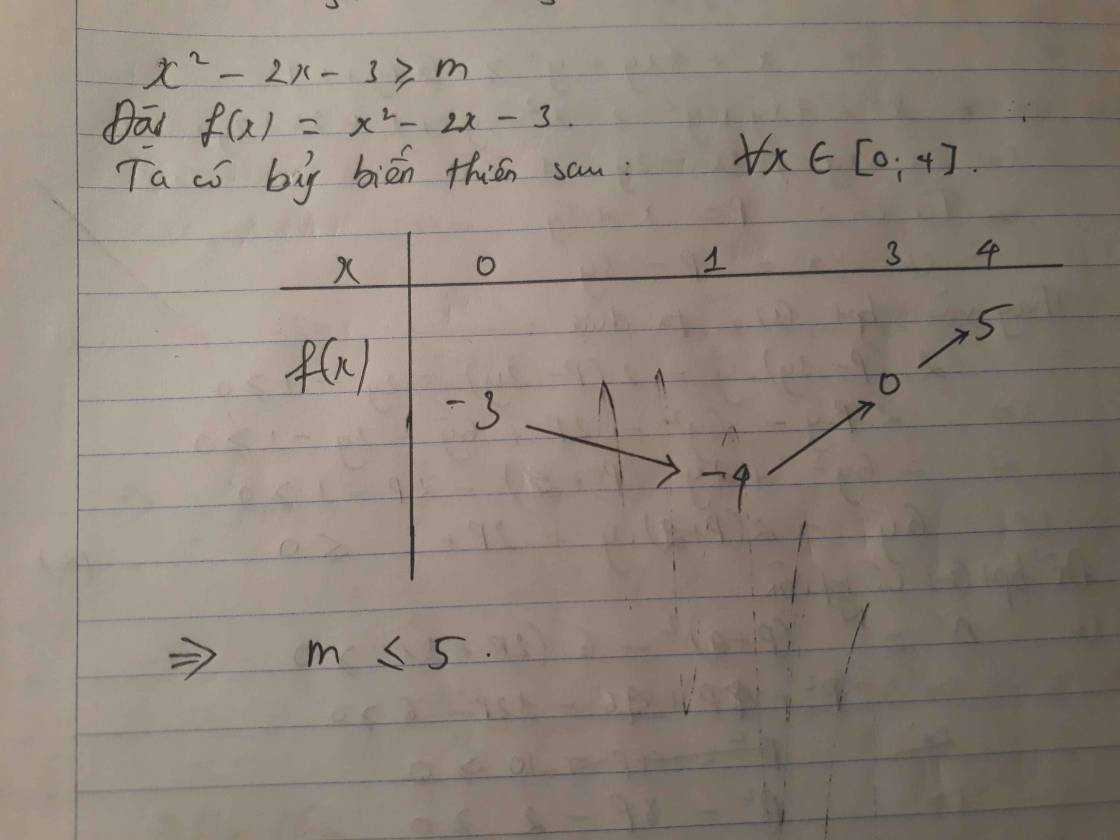  Với m <= -4 thì bpt luôn đúng với mọi x thuộc R.

Lời giải:
Đặt $\sqrt{3}+\sqrt{2}=a; \sqrt{3}-\sqrt{2}=b$. Khi đó:

$a-b=2\sqrt{2}; a+b=2\sqrt{3}; ab=1$

Khi đó:

$a^2+b^2=(a+b)^2-2ab=(2\sqrt{3})^2-2=10$

Có:

$A=(\sqrt{3}+\sqrt{2})^5-(\sqrt{3}-\sqrt{2})^5$

$=a^5-b^5=(a-b)(a^4+a^3b+a^2b^2+ab^3+b^4)$

$=(a-b)(a^4+a^2+1+b^2+b^4)$
$=(a-b)[(a^2+b^2)^2-2a^2b^2+(a^2+b^2)+1]$

$=(a-b)[(a^2+b^2)^2+(a^2+b^2)-1]$
$=2\sqrt{2}(10^2+10-1)=218\sqrt{2}$

$\Righarrow a=0; b=218; c=2$

$\Rightarrow a+b+c=220$

\(\lim\sqrt{\dfrac{9^n+3^{n+1}}{5^n+9^{n+a}}}=\lim\sqrt{\dfrac{1+3.\left(\dfrac{1}{3}\right)^n}{\left(\dfrac{5}{9}\right)^n+9^a}}=\sqrt{\dfrac{1+0}{0+9^a}}=\dfrac{1}{3^a}\)

\(\Rightarrow\dfrac{1}{3^a}< \dfrac{1}{2187}\Rightarrow a>log_32187=7\) 

Có \(2023-8+1=2016\) số

\(f\left(x\right)+f\left(1-x\right)=\dfrac{9^x}{9^x+3}+\dfrac{9^{1-x}}{9^{1-x}+3}=\dfrac{9^x}{9^x+3}+\dfrac{9}{9+3.9^x}\)

\(=\dfrac{9^x}{9^x+3}+\dfrac{3}{9^x+3}=1\)

\(\Rightarrow P=f\left(\dfrac{1}{2014}\right)+f\left(\dfrac{2023}{2024}\right)+...+f\left(\dfrac{1011}{2024}\right)+f\left(\dfrac{1013}{2024}\right)+f\left(\dfrac{1012}{2024}\right)\) 

\(=1+1+...+1+f\left(\dfrac{1}{2}\right)=1011+\dfrac{\sqrt{9}}{\sqrt{9}+3}=\dfrac{2023}{2}\)

Trong mp(SAB), gọi M là giao điểm của SG với AB

Trong mp(SBC), gọi N là giao điểm của SO với BC

Xét ΔSAB có

G là trọng tâm

M là giao điểm của SG với AB

Do đó: M là trung điểm của AB

=>\(SG=\dfrac{2}{3}SM\)

Xét ΔSBC có

O là trọng tâm

SO cắt BC tại N

Do đó: N là trung điểm của BC

=>\(SO=\dfrac{2}{3}SN\)

Xét ΔSMN có \(\dfrac{SG}{SM}=\dfrac{SO}{SN}=\dfrac{2}{3}\)

nên GO//MN

GO//MN

\(MN\subset\left(ABC\right)\)

GO không thuộc mp(ABC)

Do đó: GO//(ABC)

Sửa đề: Hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB

a: Xét hình thang ABCD có

M,N lần lượt là trung điểm của AD,BC

=>MN là đường trung bình của hình thang ABCD

=>MN//AB//CD

MN//AB

\(AB\subset\left(SAB\right)\)

MN không thuộc mp(SAB)

Do đó: MN//(SAB)

b: Đề sai rồi bạn

1. Ta chia các số thành 3 tập \(A=\left\{3;6\right\};B=\left\{1;4\right\};C=\left\{2;5\right\}\) có số dư khi chia 3 lần lượt là 0,1,2

Số chia hết cho 3 khi tổng các chữ số chia hết cho 3 \(\Rightarrow\) các chữ số phải được tạo thành bằng cách lấy 1 số từ tập A, 1 chữ số từ tập B, 1 chữ số thuộc tập C

\(\Rightarrow2.2.2=8\) cách chọn

Hoán vị 3 chữ số: \(3!=6\) cách

\(\Rightarrow8.6=48\) số thỏa mãn

2. Câu này đề là cắt Ox, Oy hay cắt "trục Ox, Oy" hay cắt "tia Ox, Oy" nhỉ?

Nếu là trục thì có vài trường hợp cần xét, tia thì chỉ cần xét 1 trường hợp thôi

2.

Do đường thẳng cắt tia Ox, Oy tại A và B, gọi \(A\left(a;0\right)\) và \(B\left(0;b\right)\) với \(\left\{{}\begin{matrix}0< a< 3\\0< b< 2\end{matrix}\right.\)

Phương trình đường thẳng dạng đoạn chắn: \(\dfrac{x}{a}+\dfrac{y}{b}=1\)

Do đường thẳng qua M nên:

\(\dfrac{3}{a}+\dfrac{2}{b}=1\Leftrightarrow b=\dfrac{2a}{a-3}\)

\(\Rightarrow S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}ab=\dfrac{a^2}{a-3}=\dfrac{\left(a-3\right)\left(a+3\right)+9}{a-3}\)

\(S=a+3+\dfrac{9}{a-3}=a-3+\dfrac{9}{a-3}+6\ge2\sqrt{\dfrac{9\left(a-3\right)}{a-3}}+6=12\)

Dấu = xảy ra khi \(a-3=\dfrac{9}{a-3}\Rightarrow a=6\Rightarrow b=4\)

\(\Rightarrow\dfrac{x}{6}+\dfrac{y}{4}=1\Leftrightarrow2x+3y-12=0\)

đâu

câu hỏi đâu ?????????????

1. 

3 mệnh đề B, C, D đúng, chỉ có mệnh đề A sai

2.

\(y'=4x-6\Rightarrow y'\left(3\right)=6\)