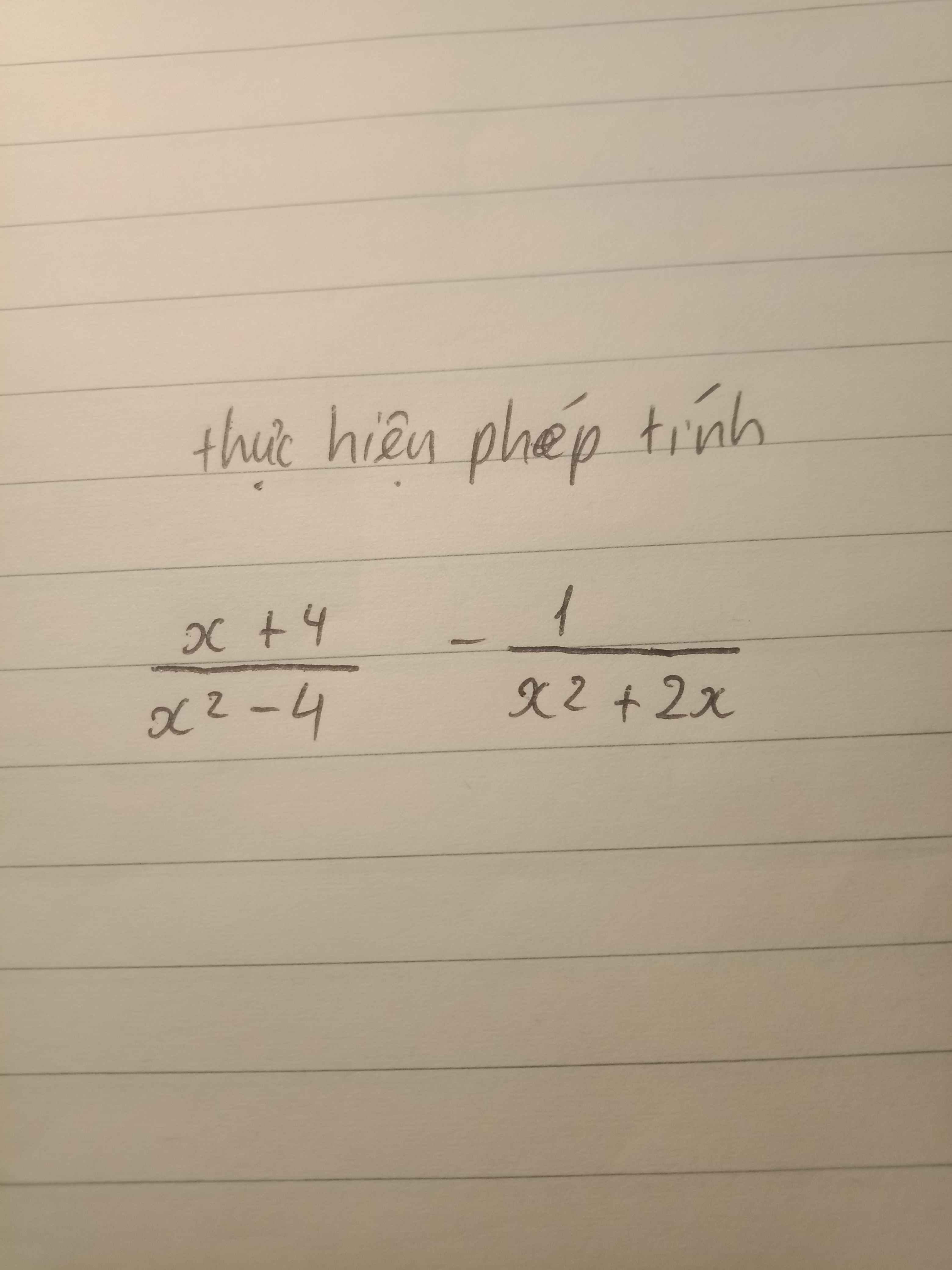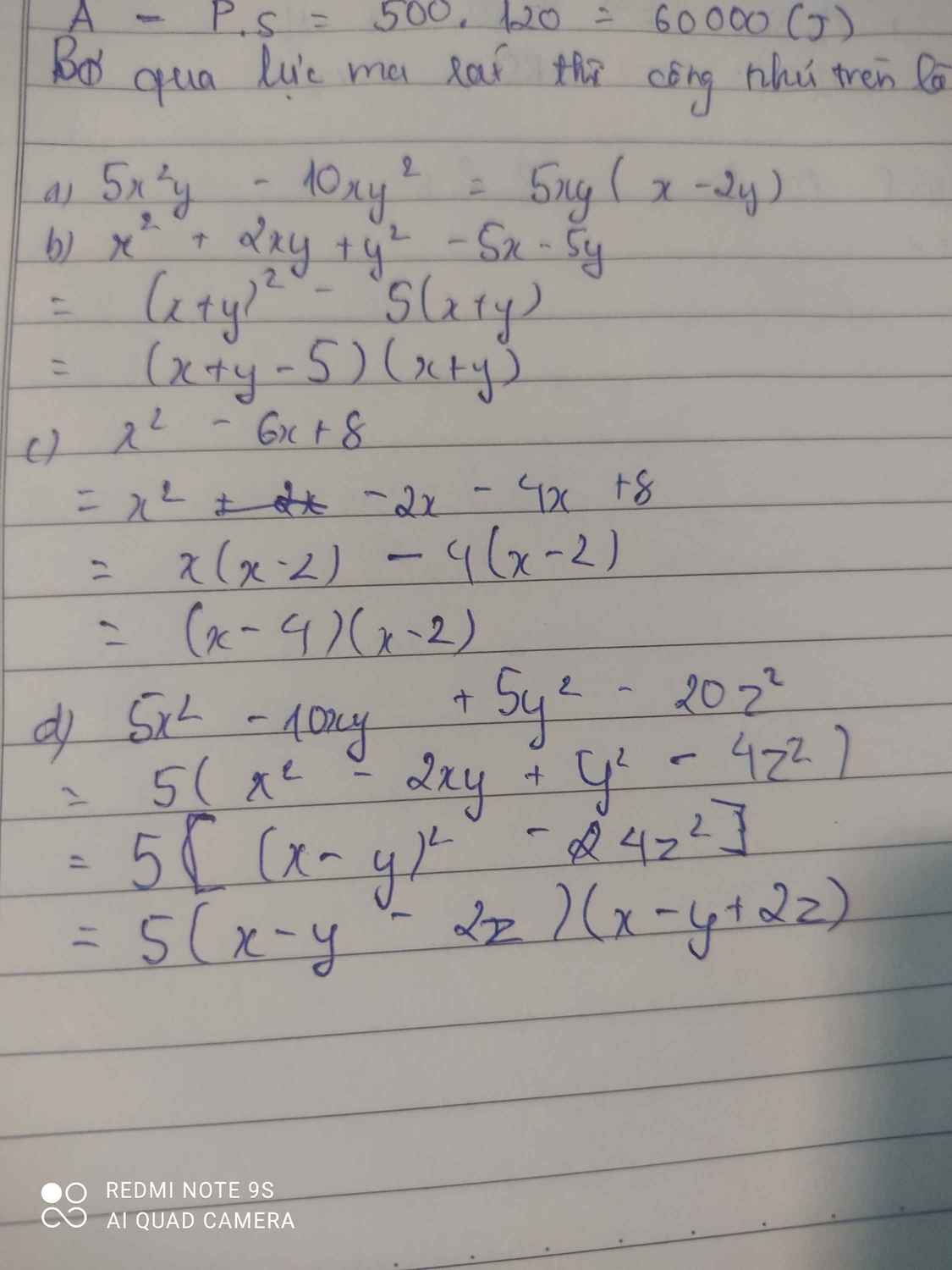\(\dfrac{18}{\left(x-3\right)\left(x^2-9\right)}\)-\(\dfrac{3}{x^2-6x+9}\)-\(\dfrac{x}{x^2-9}\)
Bài 6: Phép trừ các phân thức đại số
\(=\dfrac{18}{\left(x-3\right)^2\cdot\left(x+3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{18-3x-9-x^2+3x}{\left(x-3\right)^2\cdot\left(x+3\right)}\)
\(=\dfrac{-x^2+9}{\left(x-3\right)^2\cdot\left(x+3\right)}=\dfrac{-1}{x-3}\)
Đúng 1
Bình luận (0)
\(\dfrac{1}{3x-2}\)-\(\dfrac{1}{3+2x}\)-\(\dfrac{3x-6}{4-9x^2}\)
Sửa đề: \(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{4-9x^2}\)
\(=\dfrac{3x+2-3x+2+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{1}{3x-2}\)
Đúng 1
Bình luận (1)
\(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right)\):\(\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)
\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)
\(=\dfrac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3x-9-x^2}{3x\left(x+3\right)}\)
\(=\dfrac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{-\left(x^2-3x+9\right)}\)
\(=\dfrac{-3}{x-3}\)
Đúng 3
Bình luận (0)
\(=\left(\dfrac{9}{x\left(x^2-9\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)
\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1\cdot x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{\left(x-3\right)\cdot3}{3x\left(x+3\right)}-\dfrac{x^2}{3x\left(x+3\right)}\right)\)
\(=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3x-9-x^2}{3x\left(x+3\right)}\)
\(=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{3x-9-x^2}\)
\(=\dfrac{\left(9+x^2-3x\right)\cdot3x\left(x+3\right)}{x\left(x-3\right)\left(x+3\right)\cdot\left(3x-9-x^2\right)}\)
\(=\dfrac{\left(9+x^2-3x\right)\cdot3x\left(x+3\right)}{-x\left(x-3\right)\left(x+3\right)\cdot\left(-3x+9+x^2\right)}\)
\(=\dfrac{3x}{-x\left(x-3\right)}\)
\(=\dfrac{3}{-\left(x-3\right)}\)
\(=\dfrac{-3}{x-3}\)
Đúng 0
Bình luận (0)
1,x(x+y)^2-y(x+y)^2
1,x(x+y)^2-y(x+y)^2
`= x(x^2 + 2xy + y^2) -y(x^2+2xy+y^2) `
` = x^3 + 2x^2y + xy^2 - x^2y - 2xy^2 - y^3 `
Đúng 1
Bình luận (1)
`x(x+y)^2 - y(x+y)^2`
`= (x-y)(x+y)^2`
`= (x^2-y^2)(x+y)`
`= x^3 - xy^2 + x^2y - y^3`
Đúng 0
Bình luận (0)
\(=\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(=\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{x\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4x-x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+3x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x+1}{x^2-2x}\)
Đúng 3
Bình luận (0)
\(\Leftrightarrow\)\(\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{x\left(x+2\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x^2+4x-x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+3x-2}{x\left(x-2\right)\left(x+2\right)}\)
Đúng 2
Bình luận (0)
.Phân tích các đa thức sau thành nhân tử:
a) 5x2y- 10xy2
b) x2 + 2xy + y2 - 5x - 5y
c) x2 – 6x + 8
d)5x2 – 10xy + 5y2 – 20z2
\(a,5x^2y-10xy^2=5xy\left(x-2y\right)\\ b,x^2+2xy+y^2-5x-5y=\left(x+y\right)^2-5\left(x+y\right)=\left(x+y\right)\left(x+y-5\right)\\ c,x^2-6x+8=\left(x^2-2x\right)-\left(4x-8\right)=x\left(x-2\right)-4\left(x-2\right)=\left(x-2\right)\left(x-4\right)\\ d,5x^2-10xy+5y^2-20z^2=5\left(x^2-2xy+y^2-4z^2\right)=5\left[\left(x-y\right)^2-\left(2z\right)^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\)
Đúng 3
Bình luận (0)
Giải thích giùm mình đi. Mình tính sao mà ra dfrac{2left(5x-7right)}{x-2} thấy sai sai.
Đọc tiếp
Giải thích giùm mình đi. Mình tính sao mà ra \(\dfrac{2\left(5x-7\right)}{x-2}\) thấy sai sai.
\(\dfrac{-5x+7-2x+3-3x+4}{2-x}=\dfrac{-10x+14}{2-x}=\dfrac{-2\left(5x-7\right)}{2-x}=\dfrac{2\left(5x-7\right)}{x-2}.\)
Đúng 1
Bình luận (0)
3 / 2x +4, - x /x^2 - 4
\(=\dfrac{3}{2\left(x+2\right)}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x-6-2x}{2\left(x+2\right)\left(x-2\right)}=\dfrac{x-6}{2\left(x+2\right)\left(x-2\right)}\)
Đúng 1
Bình luận (0)
mọi người giúp mình 2 bài này với ạ,cảm ơn rất nhiều

Bài 5:
Xét ΔBAC có
FG//AC
nên \(\dfrac{FG}{AC}=\dfrac{BG}{BC}=\dfrac{1}{2}\)
hay AC=16(m)
Đúng 0
Bình luận (0)