Bài 5d: Bài tập ôn luyện
Nhằm chuẩn bị cho kế hoạch vay vốn lưu động trong quý IV năm N, công ty thương mại Thanh Hà gửi hồ sơ vay vốn tới chi nhánh NHTM A. Các thông tin về hoạt động kinh doanh và tình hình tài chính của công ty Thanh Hà thể hiện như sau:+ Tài sản lưu động dự trữ: Ngày 1-7-N: 2.450 triệu đồng, ngày 30-9-N: 2.550 triệu đồng.+ Số lượng sản phẩm tiêu thụ: 6.000 sản phẩm, giá bán 1,5 triệu đồng/ sản phẩm+ Giá vốn một đơn vị sản phẩm: 1 triệu đồng.+ Vốn lưu động tham gia vào kế hoạch kinh doanh gồm: Vốn...
Đọc tiếp
Nhằm chuẩn bị cho kế hoạch vay vốn lưu động trong quý IV năm N, công ty thương mại Thanh Hà gửi hồ sơ vay vốn tới chi nhánh NHTM A. Các thông tin về hoạt động kinh doanh và tình hình tài chính của công ty Thanh Hà thể hiện như sau:
+ Tài sản lưu động dự trữ: Ngày 1-7-N: 2.450 triệu đồng, ngày 30-9-N: 2.550 triệu đồng.
+ Số lượng sản phẩm tiêu thụ: 6.000 sản phẩm, giá bán 1,5 triệu đồng/ sản phẩm
+ Giá vốn một đơn vị sản phẩm: 1 triệu đồng.
+ Vốn lưu động tham gia vào kế hoạch kinh doanh gồm: Vốn tự có của công ty: 700 triệu đồng và vốn do công ty tự huy động: 100 triệu đồng.
Sau khi thẩm định các điều kiện vay vốn, chi nhánh NHTM A quyết định cho công ty Thanh Hà vay ở mức tối đa bằng 6% vốn dùng vào kinh doanh của chi nhánh; phương thức cho vay theo hạn mức. Vốn của chi nhánh ngân hàng bao gồm: Vốn huy động: 24.560 triệu đồng; Vốn đi vay: 4.540 triệu đồng; Vốn nhận điều hoà: 2150 triệu đồng. Các quỹ dự trữ chiếm 20% tổng nguồn vốn của chi nhánh, phần còn lại được dùng vào kinh doanh. Công ty sử dụng tài sản đảm bảo có giá trị 2500 triệu đồng để đảm bảo cho món vay. Tỷ lệ cho vay tối đa 70% giá trị đảm bảo.
Xác định hạn mức cho vay của NHTM đối với công ty. Biết
B LÀM ĐK BÀI NÀY CHƯA. CHO M XIN BÀI GIẢI VỚI.
Đúng 0
Bình luận (0)
tìm khoảng đồng biến và nghịch biến của hàm số y = g(x) = f(2x-4)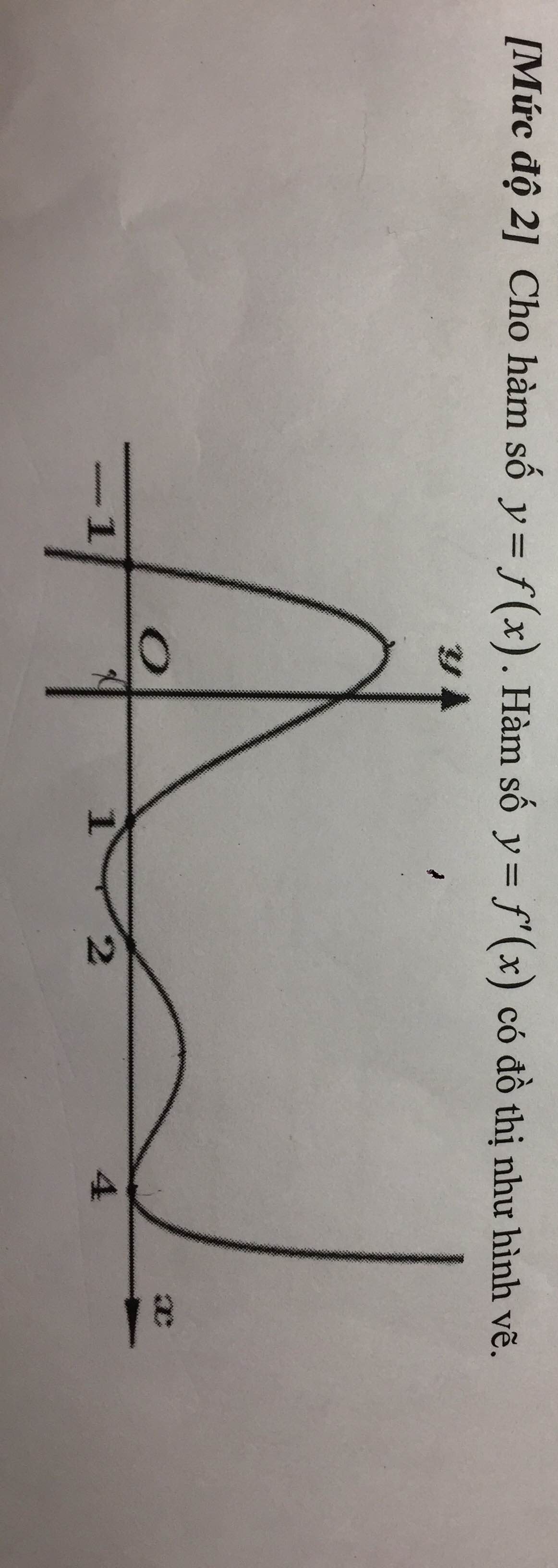
mọi người giải giúp em câu ni với nèee
Lời giải:
$g'(x)=f'(2-x)=-f'(2-x)_{2-x}$
Để $g(x)$ đồng biến thì $-f'(2-x)_{2-x}>0$
$\Leftrightarrow f'(2-x)_{2-x}< 0$
\(\Leftrightarrow \left[\begin{matrix} 2-x< -1\\ 1< 2-x< 4\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x>3\\ -2< x< 1\end{matrix}\right.\)
Vậy $g(x)$ đồng biến trên $(3;+\infty)$ và $(-2;1)$
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD có đáy là hình vuông cạnh \(a\sqrt{2}\) . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy . Tính thể tích khối chóp S.ABCD ?
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{1}{3}SH.AB^2=\dfrac{1}{3}.\dfrac{a\sqrt{6}}{2}.2a^2=\dfrac{a^3\sqrt{6}}{3}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật vs AB = \(a\sqrt{3}\) , AD = a, cạnh SA có độ dài băngg 2a và vuông góc với mặt phẳng đáy . Tính thể tích khối chóp S.BCD?
\(V_{SBCD}=\dfrac{1}{2}V_{SABCD}=\dfrac{1}{6}.SA.AB.AD=\dfrac{a^3\sqrt{3}}{3}\)
Đúng 0
Bình luận (0)
Tập hợp tất cả các giá trị thực của tham số m để hs y= \(\dfrac{-1}{3}x^3+x^2+mx-2019\) nghịch biến trên khoảng (0 ; dương vô cùng)
\(f'\left(x\right)=-x^2+2x+m\)
Để hs y = f(x) nghịch biến trên khoảng (0; dương vc)
\(f'\left(x\right)\le0\forall x\in\left(0;+\infty\right)\)
\(-x^2+2x+m\le0\)
\(m\le x^2-2x\)
\(m\le-1\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hs y = (m+1).x^4 - mx^2 +3 có 3 điểm cực trị.
Hàm có 3 điểm cực trị khi và chỉ khi:
\(-m\left(m+1\right)< 0\Rightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tất cả các gía trị thực của tham số m để hs y= mx^4 + 2(m-1).x^2 + 2 có 2 điểm cực tiểu và 1 điểm cực đại.
Hàm có 2 cực tiểu và 1 cực đại khi:
\(\left\{{}\begin{matrix}m>0\\2\left(m-1\right)m< 0\end{matrix}\right.\)
\(\Rightarrow0< m< 1\)
Đúng 0
Bình luận (0)