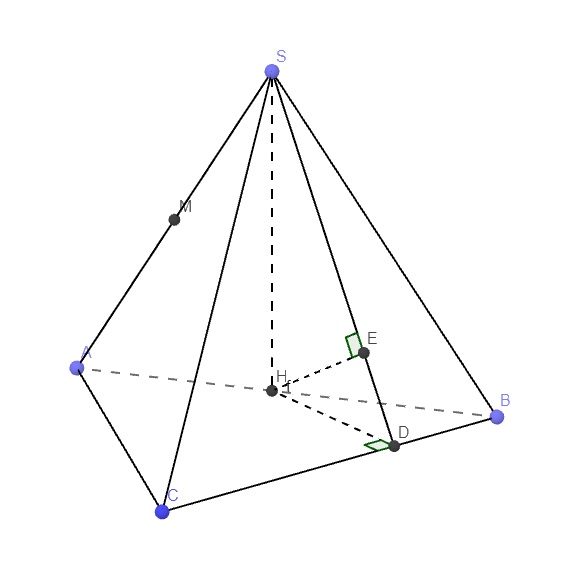
Do M là trung điểm SA, H là trung điểm AB \(\Rightarrow HM\) là đường trung bình tam giác SAB
\(\Rightarrow HM||SB\Rightarrow HM||\left(SBC\right)\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)\)
Trong mp (ABC) từ H kẻ \(HD\perp BC\), trong mp (SHD) từ H kẻ \(HE\perp SD\)
\(\Rightarrow HE\perp\left(SBC\right)\Rightarrow HE=d\left(H;\left(SBC\right)\right)\)
\(HD=HB.sinB=\dfrac{a}{2}.sin60^0=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng trong tam giác vuông SHD:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HD^2}\Rightarrow HE=\dfrac{SH.HD}{\sqrt{SH^2+HD^2}}=\dfrac{a\sqrt{51}}{17}\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=HE=\dfrac{a\sqrt{51}}{17}\)