ΔABC có AB=5cm, AC=8cm, BC=7cm tìm số đo các góc của Δ ABC toán 9
Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\\ \Rightarrow\widehat{A}=60^o\\ cosB=\dfrac{AB^2+BC^2-AC^2}{2.AB.BC}=\dfrac{5^2+7^2-8^2}{2.5.7}=\dfrac{1}{7}\\ \Rightarrow\widehat{B}=81^o47'\\ cosC=\dfrac{AC^2+BC^2-AB^2}{2.AC.BC}=\dfrac{8^2+7^2-5^2}{2.8.7}=\dfrac{11}{14}\\ \Rightarrow\widehat{C}=38^o13'\)
Đúng 1
Bình luận (0)
\(cosA=\dfrac{5^2+8^2-7^2}{2\cdot5\cdot8}=\dfrac{1}{2}\)
=>góc A=60 độ
AB/sinC=AC/sinB=BC/sinA
=>5/sinC=8/sinB=7/sin60
=>góc C=38 độ; góc B=82 độ
Đúng 0
Bình luận (0)
Cho tam giac ABC vuông tại A,đcao AH,biết AH=6cm, góc ABC = 60 độ
Tính độ dài AB và diện tích tam giác AHCsin B=AH/AB
=>6/AB=sin60
=>\(AB=4\sqrt{3}\left(cm\right)\)
=>HB=2 căn 3(cm)
=>HC=8 căn 3(cm)
\(S_{AHC}=\dfrac{1}{2}\cdot8\sqrt{3}\cdot6=24\sqrt{3}\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 15 cm, HC = 9 cm. Tính chu vi tam giác ABH và góc B là tròn đến độ.
\(BC=\dfrac{15^2}{9}=25\left(cm\right)\)
BH=25-9=16cm
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
AB=căn(16^2+12^2)=20cm
C=16+12+20=28+20=48cm
Xét ΔABC vuông tại A có sin B=AC/BC=3/5
nên góc B=37 độ
Đúng 0
Bình luận (0)
Một khúc sông rộng 400m. Một con thuyền với vận tốc 6km/h vượt qua khúc sông đó mất 5 phút. Tính góc tạo bởi đường đi của con thuyền với bờ sông
Gợi ý giải:
Con chú ý đổi đơn vị: $5$ phút = $\dfrac1{12}$ giờ.
Quãng đường thuyền đi để vượt khúc sông là:
$6 . \dfrac1{12} = 0,5$ (km) = $500$ (m).
Để tính được $\widehat{A_1}$, ta tính $\widehat{A_2}$ vì $\widehat{A_2} + \widehat{A_2} = 90^{\circ}$.
Ta có: $\cos \widehat{A_2} = \dfrac{AB}{AC} = \dfrac45$.
Từ gợi ý này con tiếp tục hoàn thiện bài nhé!
Đúng 2
Bình luận (0)
Cho tam giác ABC , đường cao AH. Biết HB=√3, B= 60 độ .Giải tam giác ABH
Xét ΔABH vuông tại H có cos B=HB/AB
nên HB/AB=1/2
=>AB=2căn3 (cm)
=>AH=3(cm)
góc HAB=90-60=30 độ
Đúng 0
Bình luận (0)
giúp mình gấp với ạ
bài 1: cho tam giác ABC vuông tại A (ACAB), đường cao AH. Kẻ HD vuông góc với ACa) Biết CH4cm, BH9cm. Tính AH và diện tích tam giác AHBb) Trên tia đối của tia HC lấy điểm E sao cho HEHA. Qua E kẻ qua đường thẳng vuông góc với BC cắt AB tại F. Chứng minhdfrac{1}{AH^2}dfrac{1}{AF^2}+dfrac{1}{AB^2}bài 2: cho chiếc thang dài 4m, biết thang an toàn khi góc tạo bởi thang và mặt đất là65^o . Khi dùng thang đó thì người thợ điện phải đặt chân thang cách chân cột điện bao nhiêu mét mới an toàn?(làm tròn...
Đọc tiếp
bài 1: cho tam giác ABC vuông tại A (AC<AB), đường cao AH. Kẻ HD vuông góc với AC
a) Biết CH=4cm, BH=9cm. Tính AH và diện tích tam giác AHB
b) Trên tia đối của tia HC lấy điểm E sao cho HE=HA. Qua E kẻ qua đường thẳng vuông góc với BC cắt AB tại F. Chứng minh\(\dfrac{1}{AH^2}=\dfrac{1}{AF^2}+\dfrac{1}{AB^2}\)
bài 2: cho chiếc thang dài 4m, biết thang an toàn khi góc tạo bởi thang và mặt đất là\(65^o\) . Khi dùng thang đó thì người thợ điện phải đặt chân thang cách chân cột điện bao nhiêu mét mới an toàn?(làm tròn đến chữ số thập phân thứ 3)
Bài 3 cho tam giác ABC vuông góc tại A có AB=30cm, AC=40cm
a) giải tam giác ABC ( số đo góc làm tròn đến độ)
b) Kẻ đường cao AH. Tính AH và diện tích tam giác AHC
c) Gọi E và F lần lượt là hình chiếu của H trên AB và AC . Chứng minh: AE.AB=AF.AC
d) Chứng minh:\(AH^3\) =HE.HF.BC
Bài 3:
a: BC=50cm
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C=37 độ
=>góc B=53 độ
b: \(AH=\dfrac{30\cdot40}{50}=24\left(cm\right)\)
\(S_{ABC}=\dfrac{30\cdot40}{2}=\dfrac{1200}{2}=600\left(cm^2\right)\)
c: AE*AB=AH^2
AF*AC=AH^2
Do đó: AE*AB=AF*AC
Đúng 0
Bình luận (0)
Giải giúp mình bài này với đang cần gấp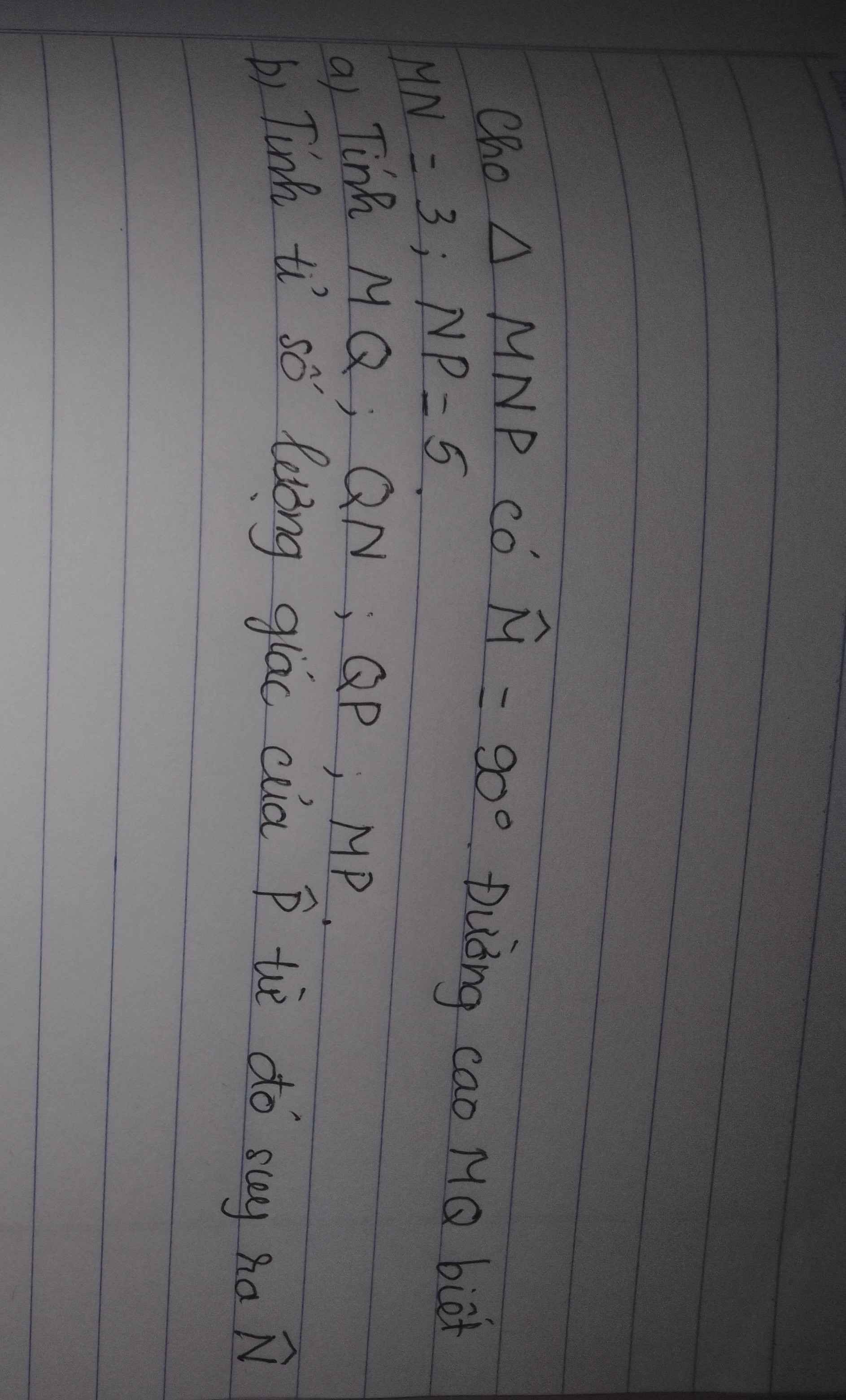
a: \(MP=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(QM=\dfrac{3\cdot4}{5}=2.4\left(cm\right)\)
\(QN=\dfrac{3^2}{5}=1.8\left(cm\right)\)
QP=5-1,8=3,2(cm)
b: sinP=cosN=MN/NP=3/5
cos P=sin N=4/5
tan P=cot N=3/4
cot P=tan N=4/3
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB = 12cm, AC = 16cm a) Giải Tam giác vuông ABC b) Kẻ đường cao AH, đường phân giác AD. Tính BD, CD, HB, HC, HD
a: BC=20cm
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C=37 độ
=>góc B=53 độ
b: \(HB=\dfrac{12^2}{20}=\dfrac{144}{20}=7.2\left(cm\right)\)
HC=20-7,2=12,8(Cm)
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
Đúng 0
Bình luận (0)






