Hệ số của x8 trong khai triển nhị thức (x+ 1/x)20 là
Bài 3: Nhị thức Niu-tơn
Lời giải:
Theo khai triển Newton:
\((x+\frac{1}{x})^{20}=\sum\limits_{k=0}^{20}C^k_{20}x^k(x^{-1})^{20-k}=\sum\limits_{k=0}^{20}C^k_{20}x^{2k-20}\)
$2k-20=8\Leftrightarrow k=14$
Hệ số của $x^8$ là: $C^{14}_{20}$
Đúng 0
Bình luận (0)
tìm hệ số x7 trong khai triển (x2 -\(\dfrac{2}{x}\))n , x≠0 biết rằng n là số nguyên dương thỏa mãn 4C3n+1 +2C2n = A3n
biết hệ số hạn thứ 3 trong khai triển ( x-1/x)^2 là y 66 tìm số hạn không chứa x trong khai triển đó
mọi người giải thích cho e chỗ hệ số ở VP với, em chưa hiểu chổ đó em cảm ơn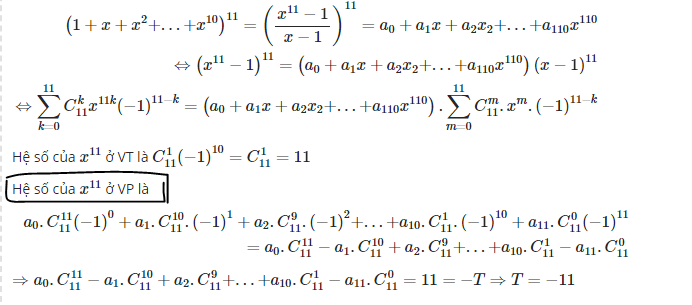
a.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(1+x^2\right)^{12}\)
b.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(2x-1\right)^{10}\)
HELP ME!
1. Tìm hệ số của x4 trong khai triển (3x+1)6
\(\left(3x+1\right)^6=\sum\limits^6_{k=0}C^k_6.\left(3x\right)^k=\sum\limits^6_{k=0}C^k_6.3^kx^k\)
\(\Rightarrow k=4\)
\(\Rightarrow\) Hệ số của \(x^4\) trong khai triển \(\left(3x+1\right)^6\) là: \(C^4_6.3^4=1215\)
Đúng 0
Bình luận (0)
Bài 1:
a.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(1+x^2\right)^{12}\)
b.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(2x-1\right)^{10}\)
Giúp mk vs ạ!!!
Trong khai triển (x-a)3 .(x+b)6, hệ số của x7 là -36 và không có số hạng chứa x8. Tìm a?
\(\left(x-a\right)^3\left(x+b\right)^6=\sum\limits^3_{k=0}C_3^kx^k.\left(-a\right)^{3-k}.\sum\limits^6_{i=0}C_6^ix^i.b^{6-i}=\sum\limits^3_{k=0}\sum\limits^6_{i=0}x^{k+i}C_3^kC_6^i\left(-a\right)^{3-k}.b^{6-i}\)
Số hạng chứa \(x^7\Rightarrow\left\{{}\begin{matrix}0\le k\le3\\0\le i\le6\\k+i=7\end{matrix}\right.\)
\(\Rightarrow\left(k;i\right)=\left(1;6\right);\left(2;5\right);\left(3;4\right)\)
\(\Rightarrow C_3^1C_6^6\left(-a\right)^2+C_3^2C_6^5\left(-a\right).b+C_3^3C_6^4b^2=-36\)
\(\Rightarrow3a^2-18ab+15b^2=-36\Rightarrow a^2-6ab+5b^2=-12\) (1)
Số hạng chứa \(x^8\Rightarrow k+i=8\)
\(\Rightarrow\left(k;i\right)=\left(2;6\right);\left(3;5\right)\)
Do ko có số hạng chứa \(x^8\Rightarrow\) hệ số của số hạng chứa \(x^8\) bằng 0
\(\Rightarrow C_3^2C_6^6\left(-a\right)+C_3^3C_6^5.b=0\)
\(\Rightarrow-3a+6b=0\Rightarrow b=\dfrac{a}{2}\)
Thế vào (1):
\(\Rightarrow a^2-3a^2+\dfrac{5}{4}a^2=-12\)
\(\Rightarrow a^2=16\Rightarrow a=\pm4\)
Đúng 1
Bình luận (1)
Câu 123 giải giúp em bằng công thức số hạng tổng quát ạ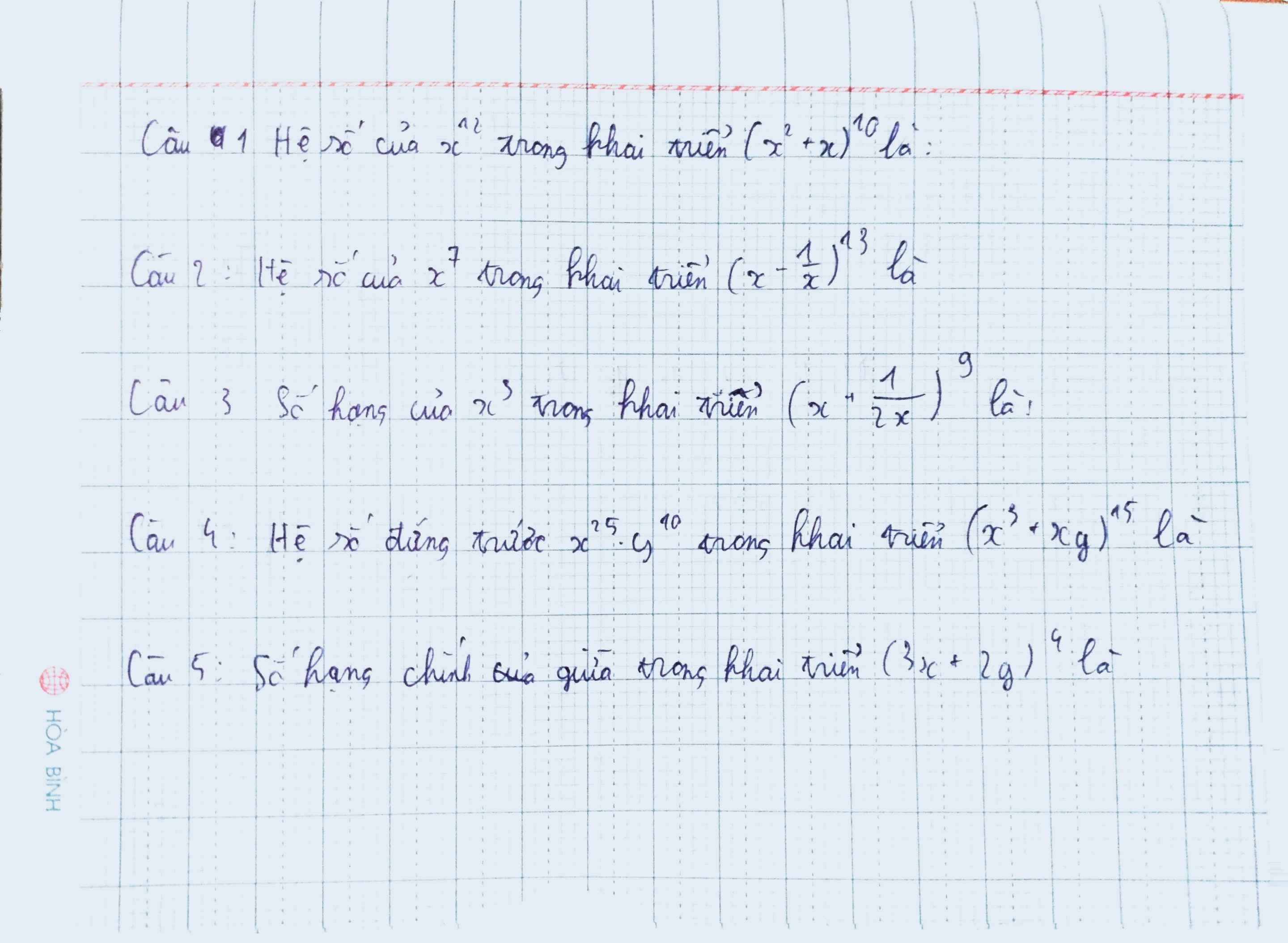
1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
Đúng 1
Bình luận (0)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)
Đúng 1
Bình luận (0)
3.
\(\left(x+\dfrac{1}{2x}\right)^9=\sum\limits^9_{k=0}C^k_9.x^{9-k}.\dfrac{1}{2^k.x^k}=\sum\limits^9_{k=0}\dfrac{C^k_9}{2^k}.x^{9-2k}\)
\(\Rightarrow9-2k=3\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển \(\left(x+\dfrac{1}{2x}\right)^9\) là: \(\dfrac{C^3_9}{2^3}=\dfrac{21}{2}\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Giúp e câu 25 đi mn
25.
\(\left(2+x\right)^7=\sum\limits^7_{k=0}C^k_7.2^{7-k}.x^k\)
\(\Rightarrow k=5\)
\(\Rightarrow\) Hệ số của \(x^5\) là: \(C^5_7.2^2=84\)
Đúng 0
Bình luận (0)

