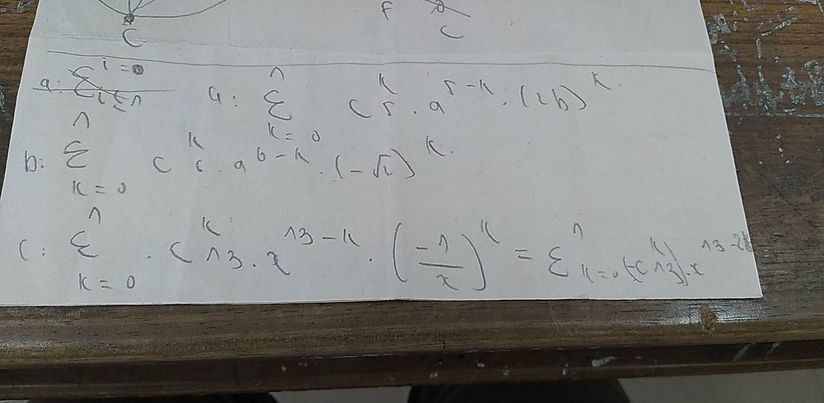Bài 3: Nhị thức Niu-tơn
Các câu hỏi tương tự
Viết khai triển theo công thức nhị thức Niu - tơn :
a) \(\left(a+2b\right)^5\)
b) \(\left(a-\sqrt{2}\right)^6\)
c) \(\left(x-\dfrac{1}{x}\right)^{13}\)
H24
21 tháng 12 2022 lúc 10:41
Cho nhị thức \(\left(2x^2+\dfrac{1}{x^3}\right)^n,\left(x\ne0\right)\) trong đó số nguyên dương n thoả mãn \(2^nC^0_n+2^{n-1}C^1_n+2^{n-2}C^2_n+...+C^n_n=59049\). Tìm số hạng chứa \(x^5\) trong khai triển.
NH
4 tháng 9 2021 lúc 15:52
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của \(\left(\dfrac{1}{2}+\dfrac{x}{3}\right)^{14}\)
Tìm hệ số của x13 trong khai triển \(f\left(x\right)=\left(\dfrac{1}{4}+x+x^2\right)^3\left(2x+1\right)^{15}\) thành đa thức
BT
22 tháng 10 2017 lúc 13:25
Các bạn giúp mình khai triển chi tiết biểu thức (a+ b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức \(\left(\sqrt{3}+\sqrt[3]{30}\right)^6\) (đến khi ra kết quả luôn nha) theo nhị thức niuton hộ mình nha
Tìm hệ số của số hạng chứa x20 trong khi khai triển nhị thức \(\left(\dfrac{1}{x^3}+x^2\right)^n\)
Biết: \(C^{n+1}_{2n+1}+C^{n+2}_{2n+1}+C^{n+3}_{2n+1}+...+C^{2n}_{2n+1}=2^{100}-1\)
Ai giải giùm bài này với !!!
BT
14 tháng 12 2016 lúc 18:56
tổng các hệ số nhị thức niuton trong khai triển \(\left(2nx+\frac{1}{2nx^2}\right)^{3n}\) bằng 64 . số hạng không chứa x trong khai triển là bao nhiêu ?
BT
22 tháng 10 2017 lúc 15:47
Các bạn giúp mình khai triển chi tiết biểu thức (a+ b)n theo nhị thức niuton đi.
Để cụ thể hơn các bạn vui lòng khai triển chi tiết biểu thức \(\left(\sqrt{3}+\sqrt[3]{30}\right)^6\) (tính ra kết quả hộ mình luôn nha) theo nhị thức niuton hộ mình nha
cho khai triển \(\left(\dfrac{x^2+2x+2}{x+1}\right)^{2020}=a_0+a_1x+a_2x^2+...+a_{2020}x^{2020}+\dfrac{b_1}{x+1}+\dfrac{b_2}{\left(x+1\right)^2}+...+\dfrac{b_{2020}}{\left(x+1\right)^{2020}}\) tính tổng \(S=b_1+b_2+...+b_{2020}\)
trong khai triển nhị thức \(\left(x\sqrt[3]{x}+x^{\dfrac{-28}{15}}\right)^n\) hãy tìm số hạng không phụ thuộc x biết rằng \(C^n_n+C^{n-1}_n+C^{n-2}_n=79\). giúp mình với ạ!